Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
Tags
- 패혈증 관련 급성 호흡곤란 증후군
- ed boarding
- nccl 설치
- first pg on this rank that detected no heartbeat of its watchdog.
- NTMs
- ERD
- GaN
- Time Series
- timellm
- nccl 업데이트
- multi gpu
- m/m/s
- 의료정보
- 대기행렬
- operation management
- 불규칙적 샘플링
- pre-trained llm
- pytorch
- Transformer
- timesfm
- 분산 학습
- moirai
- 토픽모델링
- 리뷰
- gru-d
- length of stay
- nccl 업그레이드
- irregularly sampled time series
- 딥러닝
- queueing theory
Archives
- Today
- Total
데알못정을
Ridge,Lasso regularization에 대하여 본문
728x90
[regularization]
우리는 주어진 데이터를 가지고 어떤 예측을 수행할 때 모델을 만듭니다. 즉 prediction function 인데요, 이 함수가 우리가 가진 데이터를 너무 많이 fitting 할 경우엔 흔히 일반화 성능이 나오지 않는 과적합이 발생했다고 합니다. 따라서 모델이 학습하는 과정에서 어떤 규제를 주어 과적합을 방지 하겠다는 아이디어에서 나온 개념이 바로 ridge, lasso 규제 입니다.

우리의 모델이 선형모델인 경우에, 최소자승법(OLS)을 통해 loss 를 최소화 하는 조합의 weight를 구할 수 있는데, 여기 이 w^hat 이 바로 우리가 경험한 (empirical) 데이터에 대한 loss를 최소화하는 최적의 weight입니다.

규제를 걸어줄 경우에, min 값으로 묶여 있는 이 식을 보게되면, 왼쪽 식이 loss에 대한 평균값, 오른쪽 식이 complexity measure 인데, 이 둘을 같이 minimization 하는 경우 입니다. 복잡도를 우리는 feature의 설명력을 증대하는 weight라고 볼 수 있습니다. weight를 loss와 함께 같이 줄어주면서 파라미터의 자유도를 규제하는 의미로 받아들이시면 될 것 같습니다. 그리고 lambda 는 그 복잡도 규제에 대한 비중이라고 볼 수 있어요. lambda가 커지면 커질 수록 규제의 비중이 커지는 것이죠.
[Ridge Regression]

여기서는 w에 대해 2 norm을 씌워 표현이 되었습니다. 이 measure를 사용하는것이 바로 Ridge 규제입니다.
이렇게 되면 weight도 같이 minimization이 되면서 loss도 줄이고 weight도 최소화가 되는 최적해를 찾을 수 있으므로 복잡도를 줄 일 수 있습니다.
[Lasso Regression]

Lasso regularization은 Ridge와 비슷하지만 여기서는 1-norm을 사용합니다. 1-norm을 사용하게 되면 최적 해가 sparse 한 값을 가질 수 있습니다.(즉 해가 0이 될 수도 있다.)
[Ridge vs Lasso]
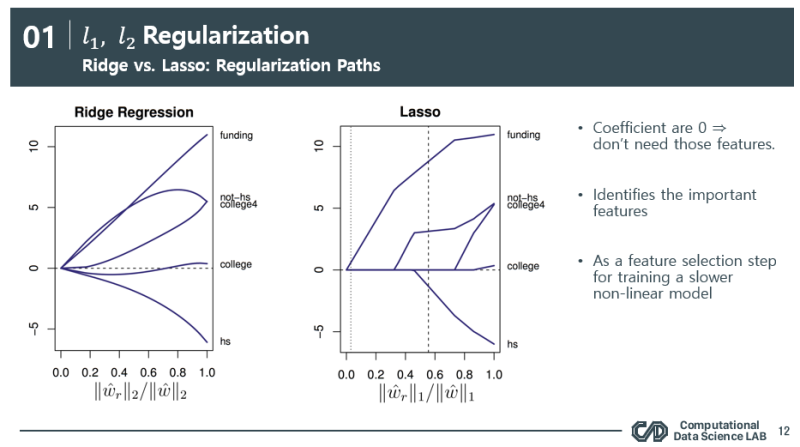
왼쪽 Y 축 : coef 값 즉 weight
오른쪽 Y 축 : feature
X 축 : 규제 weight / empirical risk minimization weight (과적합)
ridge와 lasso 둘다 regularization을 적게 할 수록 (r = ∽) 결국엔 erm weight와 같아지므로 weight가 증가(오른편으로 발산)하는 경향을 확인 할 수 있고(모델 복잡도 증가) 반대로 regularization을 많이 할수록 (r=0) 결국엔 규제를 많이 한것이니까 weight가 0으로 수렴하는 것을 알 수 있습니다. (모델 복잡도 감소)
하지만 결정적인 차이점은 lasso의 경우엔 weight를 0으로 만드는 부분이 있다는 것입니다. 이를 해석하면 ridge는 모델의 복잡도를 전체적으로 scale을 줄이게 되어 어떤 변수가 중요한 변수인지 solution을 주지 않지만 lasso의 경우엔 극단적으로 어떤 변수의 weight를 0으로 수렴시켜 중요한 변수가 아니면 내치는 기능을 하게 됩니다. 이는 각각의 장단점이 있습니다.
[Famous picture]
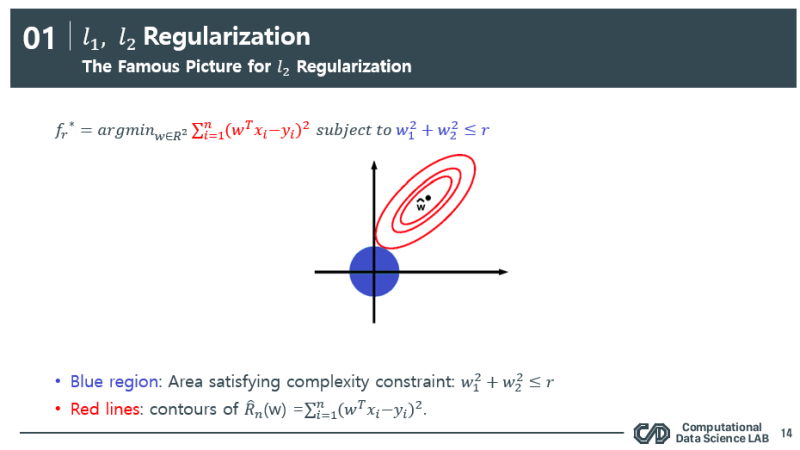
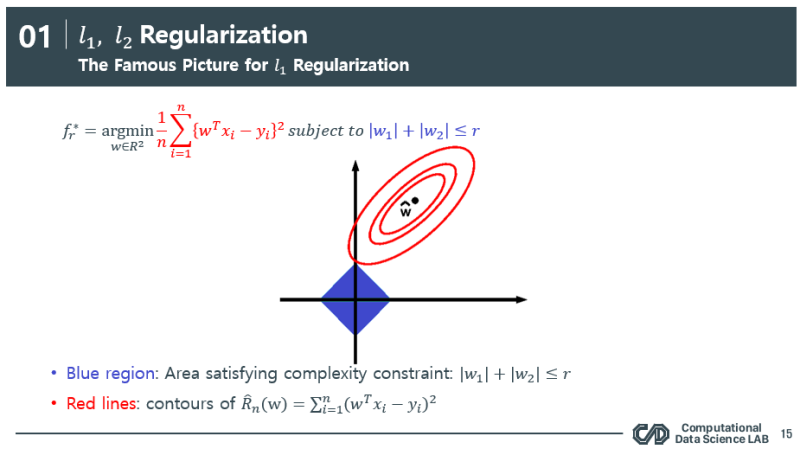
파란 영역 : 제약식 즉 규제
빨간 영역 : loss를 최소화하는 weight
따라서 규제를 통해 이 두가지의 영역이 만나는 접점에서 최적해가 결정이 됩니다.
lasso의 경우 ridge와 대비해 sparse 한 해를 갖을 수 있는 가능성이 더 크므로(축점에서 해가 발생) 해를 0으로 만들어 버리는 특징이 존재합니다.
[Elastic Net]
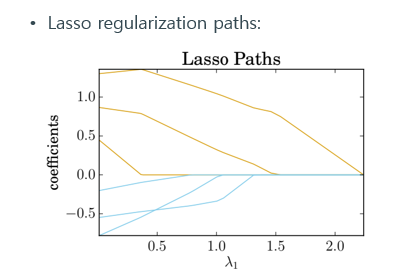
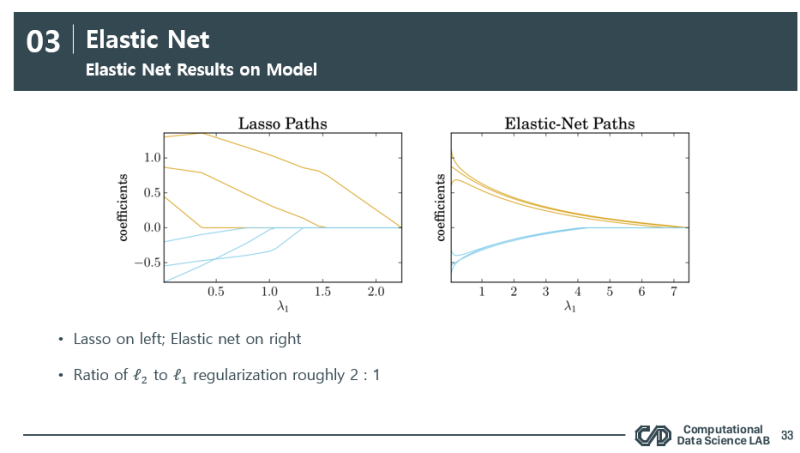
각각 노란색 path 의 변수끼리, 파란색 path의 변수끼리는 높은 상관관계가 있다고 가정헀을때, 이 그림은 lasso 규제에 대한 변수별 weight path 입니다. 이럴때 이 변수는 다중공선성을 의심할 수 있는데, 이렇게 될 경우 lasso를 사용하면 실제로 영향이 있는 변수가 A인데도 불구하고 A의 weight를 0으로 만들어 버릴 수 있는 가능성이 있는 것이죠. 따라서 이 문제의 절충안으로 나온것이 elastic net 방식입니다.

ppt 30페이지에서 보시는 것과 같이 이 규제는 lasso와 ridge를 혼합하여 규제하는 방식인데요, 이렇게 되면
너무 sparse 하지 않으면서도 적절하게 절충안을 찾게 됩니다.
그림으로 보면 직관적으로 이해가 가능합니다. 상관 관계가 높은 A와 B라는 변수가 있을 때 이 weight를 (w_1, w_2) 비슷하게 가져가면서 절충안을 찾습니다.
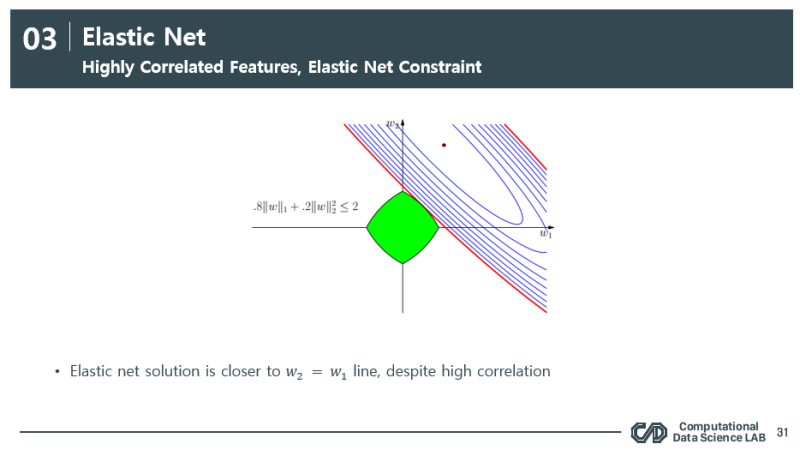
weight의 스케일을 비율로써 규제 하면서 극단적인 변화를 조금더 부드럽게 + 같은 scale로 (최대한 동등한 weight)를 갖게 끔 절충안을 찾은 모습입니다.
728x90
'Research' 카테고리의 다른 글
| DB 설계 및 HeidiSQL을 이용한 DB 구현 PART4: DB 제작 하기 (1) | 2022.09.30 |
|---|---|
| DB 설계 및 HeidiSQL을 이용한 DB 구현 PART3: SQL 개념 및 예문 (1) | 2022.09.30 |
| DB 설계 및 HeidiSQL을 이용한 DB 구현 PART2: ERD 개념 (0) | 2022.09.30 |
| DB 설계 및 HeidiSQL을 이용한 DB 구현 PART1: DB 기본 개념 (1) | 2022.09.30 |
| [ML]산학협력 프로젝트 : 이상치 탐지(Local outlier factor) (1) | 2022.09.30 |
Comments




