Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
Tags
- 의료정보
- pre-trained llm
- nccl 설치
- moirai
- GaN
- NTMs
- 분산 학습
- timesfm
- 딥러닝
- 리뷰
- first pg on this rank that detected no heartbeat of its watchdog.
- 패혈증 관련 급성 호흡곤란 증후군
- gru-d
- 토픽모델링
- m/m/s
- 불규칙적 샘플링
- pytorch
- Transformer
- timellm
- ed boarding
- ERD
- operation management
- Time Series
- nccl 업그레이드
- irregularly sampled time series
- 대기행렬
- queueing theory
- length of stay
- multi gpu
- nccl 업데이트
Archives
- Today
- Total
목록LSA (1)
데알못정을
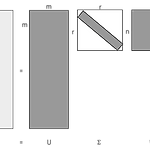 SVD(singular value decomposition) & LSA(Latent Semantic Analysis)
SVD(singular value decomposition) & LSA(Latent Semantic Analysis)
1. 특이값 분해(Singulart Value Decomposition, SVD) 특이값 분해(Singular Value Decomposition, SVD)란 실수 벡터 공간에서 A가 m $\times$ n 행렬일 때, 다음과 같이 3개의 행렬의 곱으로 분해(decomposition)하는 것을 말한다. $$A=U\sum_{}^{}V^T$$ 여기서 각 3개의 행렬은 다음과 같은 조건을 만족한다. $$U: m\times m 직교행렬$$ $$V: n\times n 직교행렬$$ $$\sum : m\times n 직사각대각행렬$$ 직교행렬(orthogonal matrix)이란 자신과 자신의 전치 행렬(transposed matrix)의 곱 또는 이를 반대로 곱한 결과가 단위행렬(identity matrix)이 되..
Topic Modeling
2022. 12. 19. 14:04
