| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- nccl 업데이트
- nccl 설치
- 토픽모델링
- gru-d
- length of stay
- 패혈증 관련 급성 호흡곤란 증후군
- 의료정보
- 대기행렬
- Transformer
- pre-trained llm
- first pg on this rank that detected no heartbeat of its watchdog.
- operation management
- pytorch
- Time Series
- irregularly sampled time series
- 리뷰
- multi gpu
- ed boarding
- timellm
- 분산 학습
- moirai
- nccl 업그레이드
- m/m/s
- GaN
- 딥러닝
- queueing theory
- 불규칙적 샘플링
- NTMs
- timesfm
- ERD
- Today
- Total
데알못정을
[Review]Attention-based Auto encoder Topic Model for Short Text 본문
[Review]Attention-based Auto encoder Topic Model for Short Text
쩡을이 2022. 12. 22. 20:30트위터 피드 글이나 stack overflow 제목 등과 같은 Short text를 가지고 토픽 모델링을 할 때 만날 수 있는 문제는 데이터 분석 시 데이터의 수가 부족할 때 만날 수 있는 문제와 비슷하다. 논문에서 저자는 전통적인 토픽 모델들이 short text에서 좋은 성능을 기대할 수 없는 이유는 short text에서 단어의 발생이 희소하기 때문이라고 말하고 있다.
논문에서 제안한 모델 Attention-based Autoencoder Topic Model, 줄여서 AATM은 1) Phrase(구문) model, 2) Attention based Auto-Encoder, 3) Ranking model로 구성되어 있다. 그림 1은 모델의 전체 구조이다.

1) Phrase model
Phrase model은 문장 내 "연어"를 처리하는 전처리 모델이다. 가령 "New york" 같은 단어는 두 단어가 독립적으로 존재할 때("New", "york")보다 두 단어를 같이 쓸 때 함축하는 정보가 더 많다. 이러한 "연어"를 고려하기 위해 Phrase model에서는 문장을 bi-gram으로 형성하여 처리했다고 했다. 근데 bi-gram이 뭔지 논문에서 언급하고 있지 않아서 이해하는데 좀 애를 먹었다.
bi-gram은 N-gram에서 N이 2일 때에 해당한다. N-gram은 N개의 연속적인 단어 나열 집합이다. 말뭉치에서 N개의 단어 뭉치 단위로 끊어서 하나의 토큰으로 간주한다. N-gram은 N을 어떻게 지정해주냐에 따라 다음과 같이 나뉜다.
Unigram(n=1), Bigram(n=2), Trigram(n=3), Ngram(n>=4)
예를 들어 "An adorable little boy is spreading smiles" 문장이 있을 때, 이를 Bigram으로 표현하면 다음과 같다.
"an adorable", "adorable little", "little boy", "boy is", "is spreading", "spreading smiles"
즉, 적절한 N은 자연스럽게 단어의 순서에서 파생되는 문맥적 의미와 연어를 동시에 고려할 수 있다.
결론적으로, 논문에서 언급된 Phrase model은 말뭉치 내의 단어의 순서와 연어를 고려하는 역할을 하며 이러한 Bigram을 파이썬 라이브러리인 gensim에 내장된 함수로 구현했다고 밝히고 있다.
2) Attention weight
Attention based Auto Encoder 단계에서는 Phrase Model의 결과로 얻은 토큰화 되어진 단어 시퀀스를 입력으로 받는다. 여기서 이루어지는 작업을 간단하게 순서로 표현하면 다음과 같다.
1. 입력된 단어 시퀀스를 수치로 임베딩하여 벡터 $w$를 얻는다.(어떤 모듈로 임베딩을 하였는지는 기술되어 있지 않았다.)
2. $w$를 기반으로 문맥을 표현해주는 문맥 임베딩 벡터 $c_s$를 계산한다. $c_s$는 다음과 같은공식으로 계산된다.
먼저 단어 시퀀스를 수치로 임베딩한 $w$가 다음과 같이 스칼라 집합 $w\in \left\{s_1, s_2,...,s_i\right\}$으로 표현할 수 있다면 $i$번째 단어 시퀀스의 임베딩 벡터는 스칼라 값 $s_i$ 이다.($w_i = s_i$)
또 단어 임베딩 벡터 $w$의 등장확률이 $p(w)$이고, 하이퍼파라미터가 $\alpha$일 때 문맥 임베딩 벡터 $c_s$는 다음과 같다.
$$c_s = \frac{1}{|s|}\sum_{w\in s}^{}\frac{\alpha}{\alpha + p(w)}$$
이게 왜 문맥 임베딩 벡터인지 설명이 안되어 있었지만 example을 만들어서 이해를 시도했다.
"i shot the sheriff" 라는 문장 $s$가 다음과 같이 임베딩되었다고 가정하자. [0.2, 0.1, -0.3, 0.9,....] 식에서 $\sum_{w\in s}^{}\frac{\alpha}{\alpha + p(w)}$ 부분에서 이 문장 $s$에 존재하는 모든 단어에 대해 등장확률을 계산한다고 생각했을 때. 하이퍼파라미터 $\alpha$는 등장확률이 0인 경우 summation term이 0으로 수렴하는 것을 방지하는 역할이라고 생각했다. 결론적으로 summation term은 [0.2, 0.1, -0.3, 0.9,....] 를 기반으로 $\alpha$와 $p(w)$로 가중치를 계산한다. 계산된 가중치는 행렬 $s$ = [0.2, 0.1, -0.3, 0.9,....]에 대해 나눠주어 $c_s$를 얻는다. 이는 즉, 일반적으로 자주 등장하는 단어에 대해서는 낮은 가중치를 부여하고, 드물게 등장하는 단어에 대해서는 높은 가중치를 부여하는 역할을 한다고 생각할 수 있다.(하이퍼파라미터 $\alpha$는 0.0001 ~ 0.001의 값이 적절하다고 한다.)
3. 1에서 계산된 $w$와 2에서 계산된 $c_s$를 사용하여 attention weight를 구한다.
$a_i=softmax(w_i^T\cdot M\cdot c_s)$
즉, 문맥 임베딩 벡터 $c_s$를 M만큼 반영한 단어 임베딩 벡터 $w$ 들의 softmax 값을 attention weight로 사용한다는 뜻이 된다.
3. Attention based Auto-Encoder

Attention based Auto-Encoder 단계는 그림 2에 해당하는 작업이 수행된다. 그림 2에서 알 수 있듯, 이 단계는 오토인코더를 활용하였음을 알 수 있다. 먼저 인코더에 해당하는 $z_s$에 입력으로 들어가는 값들은 모두 위에서 구했던 attention weight와 단어 임베딩 벡터의 선형결합으로 계산된다.
$$z=\sum_{i=1}^{n}a_iw_i$$
이를 latent vector $p_t$로 압축했다가, $r_s$로 다시 복원 한다.($p_t=softmax(w\cdot z + b)$) 압축된 $p_t$에서 $r_s$로 복원할 때 bias 값 없이 다음과 같이 계산된다.
$r_s=T^Tp_t$
이때 $T$는 weight vector이며 latent space $p_t$로부터 Topic embedding을 수행하는 역할을 한다. 즉, 문서가 토픽 정보로 부터 생성되는 상황을 연출한 것으로 생각할 수 있다.
4. Loss Function
논문에서 제안한 목적함수는 다음과 같이 2가지 항으로 이루어져 있다.
$$L'=L + \lambda L_r$$
먼저 $L$은 디코더가 $z_s$를 잘 복원하도록 유도하는 max-margin 함수이다. 이 함수가 어떤 의미인지 논문에서 기술하지 않아 이해하기 까다로웠다. hinge loss의 특징을 반영하여 나름대로의 해석을 해보려고 노력했다. 우선, 본 논문에서 정의한 $L$은 다음과 같다.
$$L=\sum_{s\in D}^{}\sum_{i=1}^{m}max(0, 1-r_sz_s + r_sn_i)$$
먼저 $n_i$는 단어를 수치로 임베딩한 단어 임베딩 집합에서 무작위로 샘플링 된 m개의 단어 벡터중 하나이다. 위 수식을 조금 수정하여 다음과 같이 나타낼 수 있다.
$$L=\sum_{s\in D}^{}\sum_{i=1}^{m}max(0, 1-(r_sz_s - r_sn_i))$$
이를 그림으로 표현하면 다음과 같다.

여기에서 만약 $r_sz_s - r_sn_i$가 1 미만의 값을 가진다면 해당 관측치에 대한 모델의 에러가 증가한다. $r_sz_s - r_sn_i$가 1 이상이라면 손실을 무시(=0)하고, 1보다 작으면 작을수록 손실 또한 크도록 유도한 것이 hinge loss형태의 본 Loss term 수식이 의미하는 바다.
여기서 $r_sz_s - r_sn_i$가 1 미만의 값을 가진다는 것은 복원 후 값 $r_s$와 원래 값 $z_s$의 유사도가 복원 후 값 $r_s$와 인코더의 입력이 아닌 아예 다른 단어 임베딩 값인 $n_i$사이의 유사도 보다 작다는 것을 의미한다. 즉, 복원을 잘 하지 못했음을 의미한다고 생각할 수 있다. 반대로, $r_sz_s - r_sn_i$의 값이 1보다 크다는 것은 복원 후 값 $r_s$와 원래 값 $z_s$의 유사도가 복원 후 값 $r_s$와 인코더의 입력이 아닌 아예 다른 단어 임베딩 값인 $n_i$사이의 유사도 보다 크다는 것을 의미하며 복원을 잘 했음을 의미한다고 생각할 수 있다. 이렇게 의도적으로 오토인코더 구조에 입력되지 않은 단어 임베딩 값을 랜덤하게 m개 추출하여(여기서 m은 배치의 갯수가 될 수 있을 것 같다.) 일종의 negative sample로써 활용하여 복원 후 값과 원래 값인 인코더의 입력값 사이의 유사도를 높이는 방향으로 오토인코더의 학습을 유도할 수 있다.
왜 일반적으로 사용하는 MSE 손실함수를 사용하지 않았을까? 그 이유를 나름대로 추론해 보자면 저자가 잠재 공간에서 토픽이 생성되어 문서를 생성한다는 의미를 모델에 담고 싶었기 때문이 아닐까 싶다. 만약 MSE를 사용하게 된다면 topic embedding vector $T$는 토픽의 정보를 담았다고 의미를 부여할 수 없을 것 같다. 결론적으로 인코더의 인풋인 문맥 정보를 고려한 단어 임베딩 벡터와 잠재 공간에서 토픽 임베딩의 영향을 받아 복원된 $r_s$사이의 유사도를 높이면서 $T$가 토픽 정보를 학습 한다는 의미를 부여할 수 있게 된다.
다음은 Loss function의 두 번째 항인 $L_r$이다. $L_r$은 [1]에서 제안한 orthogonal regularization을 그대로 사용하였으며, 이는 학습된 토픽 임베딩 $T$간의 유일성을 부여할 수 있다. 수식은 다음과 같다.
$$L_r = \left\|T_n\cdot T_n^T - I \right\|$$
먼저 orthogonal matrix(직교행렬)이란 행벡터와 열벡터가 유클리드 공간의 정규 직교 기저를 이루는 실수행렬이다. $n \times n$ 행렬 $Q$에 대해 $Q^TQ$의 결과가 Unit vector가 되는 행렬 $Q$는 orthogonal matrix이다. 이를 regularization 효과를 낼 수 있도록 위와 같이 정의하여 손실함수에 추가하여 토픽 임베딩 $T$를 orthgonal matrix로 만들어 버리면서 서로 다른 토픽을 만들어 낼 수 있다.
목적함수를 통해 학습된 Topic embedding vector $T$와 단어 임베딩 벡터 $w$ 사이의 cosine similarity를 통해 토픽으로 사용할 단어를 얻을 수 있다.
5. Ranking model
Ranking model에서는 토픽 임베딩 벡터 $T$와 단어 임베딩 벡터 $w$사이의 유사도를 기반으로 단어를 정렬해놓고 시작한다. 가령 $T_1$과 유사도가 높은 단어들의 집합이 다음과 같이 ['Fruit', 'Apple', 'Pitch',....,] 일 때, 이를 word net을 활용하여 각 단어 사이의 관계를 파악한다. (예를 들어 상위어("사과"는 "과일"에 속하니까 "과일"이 상위어), 하위어 등) 그 후 가장 상위에 있는 단어를 토픽으로 설정한다.

6. Experiment
실험에서 사용한 데이터 셋은 short text 데이터로, Web Snippet과, News 데이터 셋이다. Web Snippet은 12,340개의 8가지 범주의 웹 검색어이다. News는 7가지의 범주를 가진 짧은 뉴스기사 데이터이다.
논문에서 제안 모델의 성능을 비교하기 위해 비교 모델로 BTM, GPU-DMM, GPU-PDMM을 사용했다. 각각의 모델은 short text에서 토픽을 탐지하는 모델로써, BTM의 경우엔 bi-gram을 사용하여 토픽을 탐지하는 모델, GPU-DMM, GPU-PDMM은 각각 디리클레, 포아송 분포를 가정한 통계적 모델로 간단히 설명하고 있었다. 실험을 위해서 단어 임베딩 모듈로는 Google-News가 사전 학습된 임베딩 모델을 사용했다고 밝히고 있으며 AATM에 학습시킬 때는 위 데이터 셋을 fine tuning 했다고 한다.
1) Topic Coherence
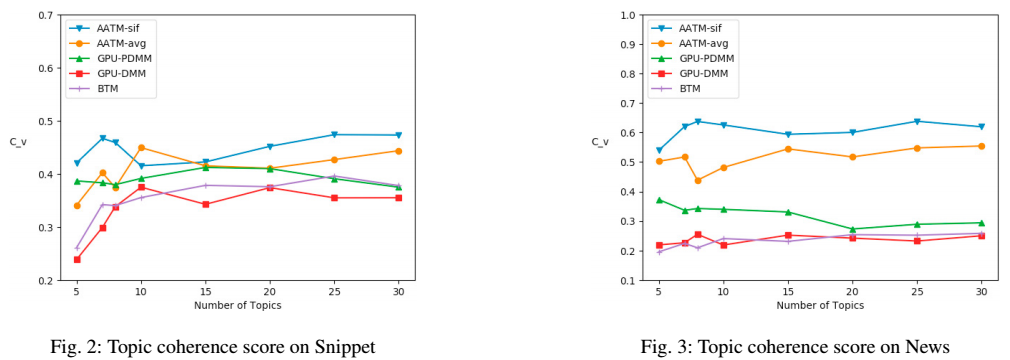
이 논문에서는 Plamtto 계산기 대신에 자연어 처리 라이브러리 gensim을 이용하여 TC 점수를 측정했다고 한다. 실험 결과 위 비교모델 보다 제안한 모델의 TC 점수가 더 높았으며 이는 attention machanism이 불필요한 정보를 토픽을 추출하는 과정에서 배제할 수 있는 역할을 했다고 해석하고 있다. 여기서 SIF방식와 avg 방식의 차이는 문맥 임베딩 벡터 $c_s$를 구할 때 단순히 문맥 임베딩 벡터로 단어 임베딩 벡터 각각을 평균처리 할 것인지, 아니면 위에서 소개한 것과 같이 구할 것인지이다. SIF 방식으로 할 경우 TC 점수가 더 높았는데 이는 SIF가 문맥 정보를 더욱 잘 학습할 수 있도록 유도하기 때문이다.
2) Classification

이 실험은 훈련과정에서 얻은 $T$행렬을 가지고 문서를 분류하는 task를 수행하는 실험이다. 실험결과는 다음과 같다. 여기서 K란 토픽의 갯수 이며, 제안된 모델인 AATM의 경우엔 오토인코더 구조에서 latent vector의 차원 수이다.
실험결과 Snippet 데이터 셋에 대해서는 비교모델의 성능 보다 제안 모델의 성능이 대부분 더 좋았다. 하지만 News 데이터 셋에 대해서는 비교 모델의 성능이 더 좋았다고 밝히고 있다. 하지만 저자는 비교 모델의 추론과정이 깁스 샘플링을 수행하는 등 모델의 추론 복잡도를 고려했을 때, 제안한 모델이 양질의 성능을 얻었다고 말하고 있다.
○정리 및 활용할 점
본 논문은 short text를 위한 토픽 모델링 알고리즘 AATM을 제안했다. Phrase model에서 bi-gram을 통한 연어 고려와 SIF를 기반으로 계산한 attention weight를 통해 짧은 문장에서도 문맥적 의미를 반영하려고 노력한 것이 인상 깊었다. 또한 오토인코더 구조를 활용하여 잠재 공간에서 토픽이 생성되는 컨셉을 연출하기 위해 MSE 손실함수가 아닌 유사도 기반의 hinge loss를 사용한 것이 신기했다. 본 모델은 짧은 문장의 토픽 추출을 위해 제안되었지만, 꼭 짧은 문장이 아니더라도, 연어를 고려한 전처리(phrase model), 단어 간의 문맥적 의미를 고려한 attention weight 계산 방법은 앞으로 토픽 모델 알고리즘을 개발할 때 있어서 반영하면 좋을 것 같다. 또한 이 논문을 통해 앞으로의 프로젝트에서 활용하고 싶은 점은 토픽에 단어를 부여할 때 word net을 사용하는 것이다. 이는 토픽 모델링 자체가 토픽에 단어를 부여할 때 있어서, 어쩔 수 없이 사람의 개입이 들어가게 되는데, word net으로 후보 단어 간의 유사도 및 계층적 구조를 밝힐 수 있으므로 토픽을 결정하는데 있어서 사람의 개입을 최대한 피할 수 있을 것 같다. 실제 프로젝트에서 토픽이 어떤 근거로 단어가 부여되었는지 이유를 기술할 때 word net을 사용한다면 단어의 계층적 구조를 시각적으로 보여주면서 이론적 근거로 사용할 수 있을 것 같다고 생각했다. 하지만 이렇게 결정한 토픽은 결국 문서 내에 존재하는 단어로 한정되며, 후보 단어 중 상위어로 쓸만한 단어가 없다면 토픽으로 결정하기는 어려울 것 같다.
참고문헌
[1]He, Ruidan, et al. "An unsupervised neural attention model for aspect extraction." Proceedings of the 55th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers). 2017.




