| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 패혈증 관련 급성 호흡곤란 증후군
- 의료 의사결정
- GaN
- 분산 학습
- ERD
- 불규칙적 샘플링
- Time Series
- NTMs
- causal inference
- 리뷰
- nccl 업그레이드
- nccl 업데이트
- gru-d
- first pg on this rank that detected no heartbeat of its watchdog.
- 인과추론 의료
- nccl 설치
- 토픽모델링
- machine learning
- causal reasoning
- doubleml
- 의료
- multi gpu
- netflix thumbnail
- causal machine learning
- pytorch
- 의료정보
- causal ml
- Transformer
- irregularly sampled time series
- 딥러닝
- Today
- Total
데알못정을
[Review] Mamba: Linear-Time Sequence Modeling with Selective State Spaces 쉽게 이해하기 본문
[Review] Mamba: Linear-Time Sequence Modeling with Selective State Spaces 쉽게 이해하기
쩡을이 2024. 3. 24. 16:11Summary

이번 포스팅에서는 최근 Long sequence data modal에서 Transformer의 성능을 앞도하고 있는 Deep State Space Model의 발전 과정과 글의 문맥적 흐름까지 이해할 수 있도록 설계된 Selective State Space Model, 그리고 그 아키텍처를 단순화한 Mamba를 알아보도록 하겠습니다. 해당 논문은 여러가지 사전 지식이 없는 상태에서 읽는 것은 (산업공학도로서)매우 힘든 일입니다. 왜냐하면 State Space Model(SSM)과 이것의 딥러닝 아키텍처로서의 사용부터, 연산을 효율적으로 하기 위한 많은 시도들을 알고 있어야, 비로소 이 논문의 motivation을 공감할 수 있고, 문제를 어떻게 해결했는지 이해할 수 있기 때문입니다. 실제 논문에서는 이러한 지식을 친절하게 설명해주지 않습니다. 제가 이 논문을 이해하기 위해 참고한 자료는 아래에 reference로 올려드리겠습니다. 아래 자료들이 이 논문을 이해하기 위한 선행 지식을 쌓기 매우 정확할 수 있습니다. 따라서 제 포스팅을 보기전에 먼저 해당 자료들을 참고하시고, 그래도 이해가 안되면 제 포스팅을 보는 것을 추천드립니다... ㅎㅎ
Reference
https://www.youtube.com/watch?v=A6aQ17oFNTQ&t=375s
https://srush.github.io/annotated-s4/
The Annotated S4
srush.github.io
https://www.youtube.com/watch?v=luCBXCErkCs
https://www.youtube.com/watch?v=h_VpKMFrxN0&t=662s
Background 1. State Space Model(SSM)
여기서 설명하는 SSM은 모두 LTI system을 가정한 SSM입니다.
State Space Model(SSM)은 시간에 따라 변화하는 시스템을 모델링하는데 사용되는 수학적 모델입니다. Dynamic system을 control하는 것이 해당 모델의 사용 목적입니다. SSM을 통해서 Dynamic system의 미래 상태를 현재 상태와 입력을 바탕으로 예측할 수 있습니다. 아래 예시는 SSM이 어떻게 dynamic system의 출력을 통제하는지 보여줍니다.
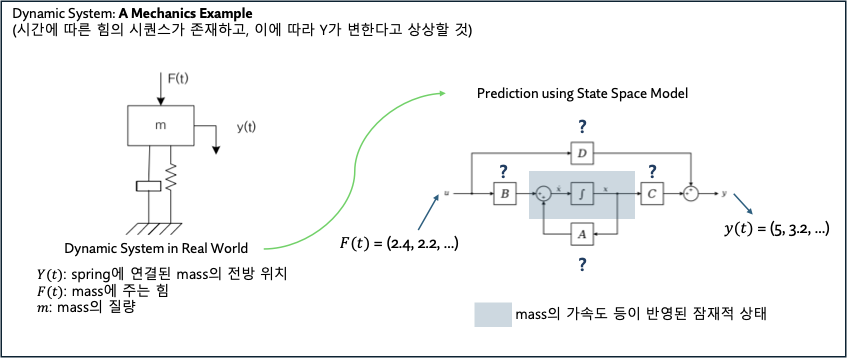
여기서 State란 어떠한 입력값들이 주어졌을 때, 시스템과 그것의 반응(출력)을 fully describe하는 최소한의 변수들의 집합입니다. 만약 시스템의 state variables가 어떤 최초의 입력 시간 $t_0$ 부터 일련의 시간 동안 $\vec{x} = [x_1(t_o), x_2(t_1),...]$ 로 정의 되어 있다면(시간에 따른 상태를 알고 있다면), 시스템의 입력 시퀀스는 시스템의 모든 future behavior를 충분히 결정할 수 있습니다.

state에 대한 표현은 다음과 같습니다.


여기서 A는 state의 dynamics를 모델링하고, B는 입력 값을 conversion하는 matrix입니다. 그리고, 식의 좌항은 state의 미분량을 나타내고 있는데, 이게 연속 시간에서의 state의 변화량을 의미합니다.(아직까지는 감이 안옵니다.)

결과적으로 system의 output은 위 과정을 통해 도출됩니다. 이때 matrix D는 0으로 처리하는데, 이는 입력 값이 출력 값에 직접적인 영향을 주는 것을 방지하기 위해서 그런다고 합니다.

Machine Learning 분야에서 사용하는 sequence data는 일반적으로 descrete sequence로 존재합니다. Waveform의 경우 일정 간격의 step size로 sampling 되는 것이 그 예시 입니다. 헬스케어에서는 중환자실에서 측정되는 vital sign을 데이터 분석에 활용하기 위해 몇 시간 단위로 resampling하여 sequence를 얻기도 합니다. 위에서 정의했던 SSM은 수식에서도 알 수 있듯이, 연속시간에서 사용할 수 있는 형태로 되어 있습니다.(입력 값이 시간에 따른 매개 함수이기 때문)
이러한 Continuous-time SSM을 discrete input sequence에 적용하기 위해서, 파라미터 A,B,C를 약간 수정하면 다음과 같습니다. 이는 Bilnear transform을 통해 수행 가능합니다.

아래는 해당 파라미터를 이용한 이산화된 SSM과 원래 SSM을 비교한 장표입니다.

이제 연속 함수를 입력 받아 연속 함수를 출력(function to function)하는 것이 아니라, sequence-to-sequece로의 mapping으로 그 관점이 바뀌게 됩니다. 연속 시간과 다르게, 이산 시간에서는 현재 시점의 상태($x_t$)가 이전 시점($x_{t-1}$)의 상태의 영향을 받게 됩니다. 또한 Discrete time SSM의 형태는 RNN의 동작 구조와 매우 비슷하게(똑같나?) 생겼습니다. 따라서 이러한 형태를 SSM의 Recurrent Representation이라고 부릅니다.
하지만 매우 긴 시퀀스를 처리해야 하는 Task에서 Recurrent representation을 통해 모델링하는 것은 매우 비효율적입니다. 왜냐면, Sequence의 각 요소를 시간에 따라 1개씩 넣어주여야 하기 때문입니다. 이러한 문제를 극복하기 위해서 SSM을 recurrent representation말고, Convolutation Representation으로 모델링하면, 입력 sequence를 한번에 처리할 수 있는 이점이 있습니다. Convolution representation을 유도하는 과정은 아래와 같습니다.

매우 복잡해 보이지만, 사실은 $x_{-1}$을 0으로 두고, 하나씩 넣어서 얻은 값을 재귀적으로 넣어주면 kernel 또는 filter라고 부르는 matrix를 얻을 수 있습니다. 이는 LTI system을 가정했기 때문에 가능한 부분입니다.

SSM의 다양한 표현 방법을 요약한 그림입니다. SSM은 학습을 할 때는 Convolution representation으로 한번에 학습하고, 추론 시, Recurrent representation 방식으로 바꿔서 사용할 수 있습니다.
여기까지나 SSM에 대한 기본적인 설명입니다. 아직, 파라미터 A,B,C를 업데이트 하는 부분은 없고, 모두 고정되어 있습니다. 처음 여기까지 공부를 했을 때 도대체 학습은 어떻게 하는 것인지 정말 모르겠더라구요. 따라서 Reference에 달아둔 Annoted S4라는 제목을 가진 저자의 블로그를 참고하여 SSM이 어떻게 딥러닝 아키텍처에 적용되는지 코드를 통해 살펴보았습니다.


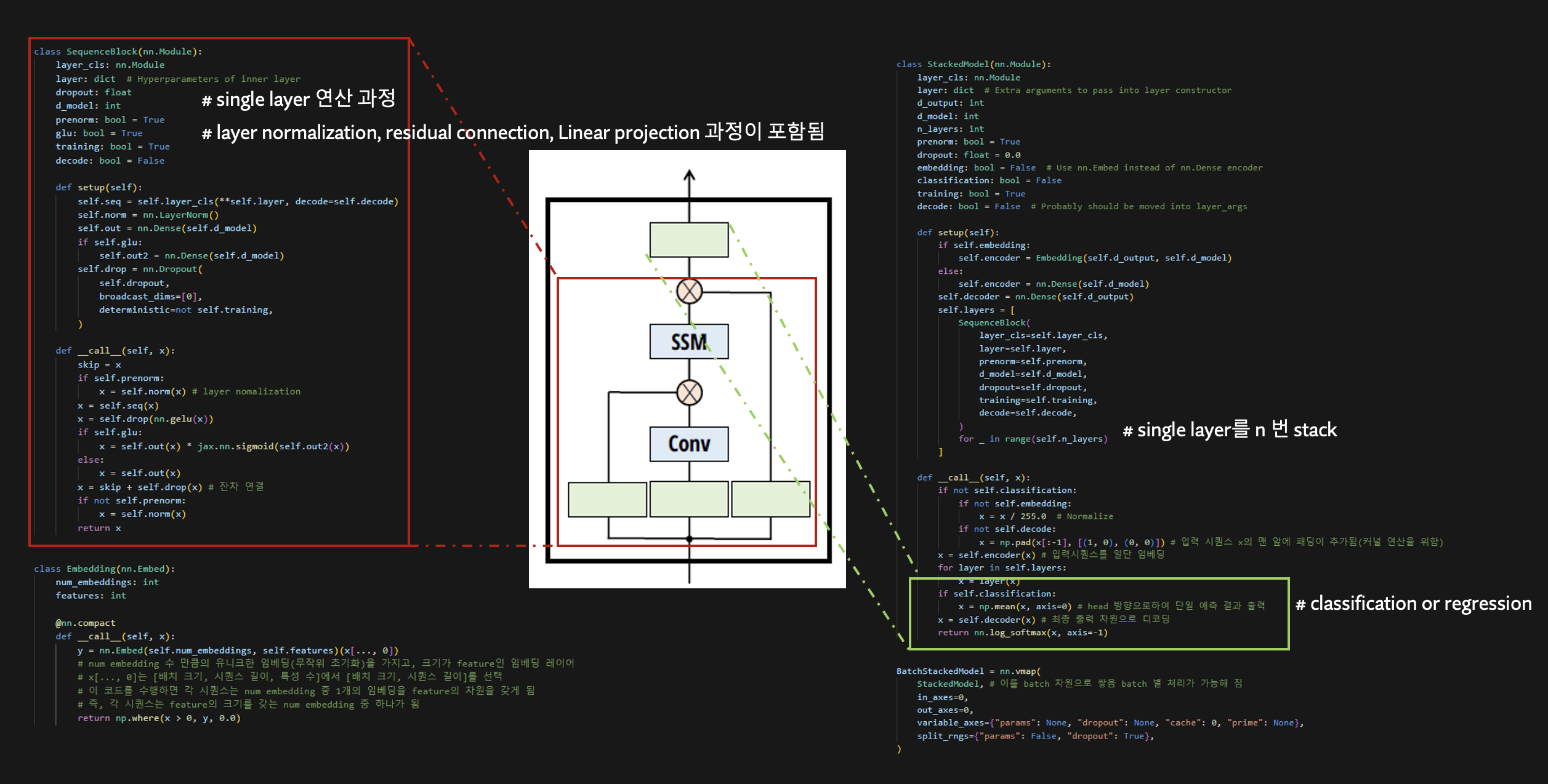
결론적으로 파라미터 A, B, C는 random하게 초기화 시켜놓고, 입력 값을 넣어준 뒤, 출력된 값을 linear projection한 네트워크를 여러번 쌓아서 출력 값을 도출하는 과정인 것을 확인할 수 있습니다. 따라서, SSM의 파라미터 A, B, C는 학습되는 파라미터가 아닌 것으로 결론을 낼 수 있습니다. 이러한 맥락은 실제로 성능적인 문제를 유발했고, background 2, 3에서 언급할 hippo matrix, LSSL의 제안으로 이어집니다. 하지만 이도 역시 Kernel을 연산하는 것이 메모리적으로 비효율적이라는 문제가 있기 때문에, background 4에서 언급할 S4의 제안으로 이어지고, S4에서 존재하는 문제를 다시 해결한 논문이 Mamba에서 다루는 내용입니다.
Background 2. HiPPO: Recurrent memmory with Optimal Polynomial Projection
DeepSSM에서 볼 수 있었던 문제는 파라미터 A, B, C를 random하게 초기화 해놓고 모델링을 하다보니, 현재 처리하고 있는 token보다 더욱 이전에 들어왔던 token을 까먹는 것이었습니다.(Long term dependency) 따라서 과거의 모든 시퀀스를 잘 기억할 수 있는 matrix를 찾아서 파라미터 A, B, C를 학습하는 것이 HiPPO의 목적이었습니다.
어떤 measure $\mu$(두 함수의 차이를 측정하는 어떠한 것)가 있을 때, polynomial basis function $\mathcal G$는 continuous function 즉, 시퀀스 $f$를 잘 매핑 하도록 아래와 같이 추정합니다. 여기서 $\mu$는 시간에따라 다르게 주는 가중치이고, $g^t$는 coefficient c와 결합합니다.


위 그림 (1)에서 function $f$는 Time $t$에 따라 존재하고 있고, HiPPO framework의 작동은 (2)에서 묘사 되어 있습니다. 각 포인트 마다 $f_t$와의 가장 작은 차이를 갖는 basis function $g$의 coefficient를 찾아서 복구하는 방식으로 작동합니다. 이 논문의 contribution은 (3)처럼, g의 계수인 $c(t)$ 업데이트 룰을 ODE 꼴로 만든 것에 있는데, 이 방정식을 풀어서 표현했을 때, (4) 처럼 discrete time SSM 구조가 나오기 때문입니다.

여기서 생각할 수 있는 것은, 우리는 입력값 $f$를 알고 있고, $\mu$도 정의해줄 수 있고, $c(t)$도 구할 수 있기 때문에, matrix A, B를 구할 수 있습니다. 이러한 matrix는 전체 입력을 잘 복원하도록 하는 계수로 추정된 matrix기 때문에, 전체 시퀀스를 잘 기억할 수 있는 A, B가 되고, (4)에서 식은 SSM 형태를 나타내고 있으니 A, B를 구해서 넣어주면, 전체 시퀀스를 까먹어 버리는 기존의 문제를 해결할 수 있다는 것을 알 수 있습니다.

Background 3. Combining Recurrent, Convolutional and Continuous time Models with Linear State Space Layers(LSSL)
LSSL은 A matrix를 HiPPO matrix로 바꿔서 구현한 것입니다. 이렇게 바꿨더니, benchmark task인 sequentialMNIST에서 기존 60%였던 정확도를 98%까지 끌어올릴 수 있었고, Regression 문제에서도 Transformer 보다 더 좋은 성능을 낼 수 있었습니다.

Background 4. Efficiently Modeling Long Sequences with Structured State Spaces(S4)
HiPPO로 deepSSM의 장기 의존성 문제를 해결했음에도, 여전히 남아 있는 문제는 matrix A를 시퀀스 길이만큼 거듭 제곱하는 것에서 계산 효율성이 매우 낮다는 것이었습니다. 실제 위에서 kernel representation의 kernel filter를 보면 시퀀스 길이 만큼 A를 거듭제곱하는데요, 행렬의 반복적인 곱으로 인한 계산량을 줄이기 위해서 간단히 생각할 수 있는 것은 A를 diagonalize하는 것입니다.
$X = V X\tilde$ 라 하고, 대입하고, 양변에 $V$의 inverse를 취해주면 $Y = CV\tild$가 됩니다. 계산을 효율적으로 하기 위해서 $V^{-1} A V$ 가 diagonal 이면 거듭 제곱해도 computation이 쉬워지게 될 것입니다. 이러한 $V$를 찾는 것이 이 논문의 핵심 내용입니다.


복잡한 수식 제끼고,, 아무튼 계산량이 attention 보다도 줄어들었습니다.
Selective SSMs(S6)
드디어 본 논문입니다. 시퀀스 모델링의 근본적인 문제는 context를 smaller state로 잘 압축하는 것에 있고, Trade-off 문제를 가지고 있습니다. 예를들어 Attention은 effective하나, inefficient 합니다. 그 이유는 inference를 위해 전체 context(i.e. K, V cache)를 메모리에 모두 저장하고 있어야 하기때문입니다.
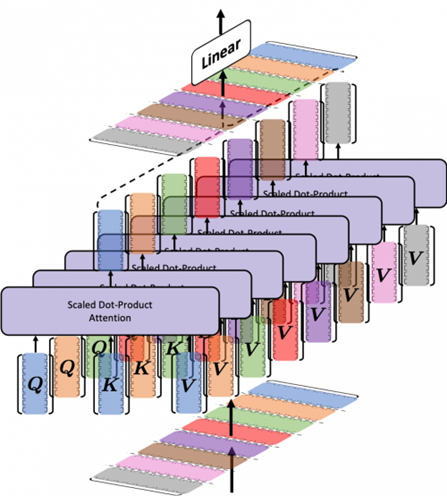
위 그림처럼, 각 입력 토큰에 대한 query, key, value를 모두 갖고 있어야 합니다. 이렇게, 전체 context를 저장하고 있는 방식은 slow linear-time inference, quadratic-time training을 유발합니다.
반대로, Recurrent models(SSMs)는 시퀀스 전체에 대해서 유한한 hidden state를 가집니다. 이는 constant time inference, linear time training으로, efficient하나, context가 그러한 state에 얼마나 잘 압축이 되는가에 성능이 달려있기 때문에 ineffective 합니다.
실제로, SSMs 기반 모델은 다음 세 가지 Task 중 두 가지 Task에서 모델링에 실패하였습니다.
(하얀색 블록은 시퀀스에서 Masking을, 검정색 블록은 예측해야 할 시퀀스를 의미)
1. Copying Task: Success
- 입력된 시퀀스는 기억해야 할 시퀀스이고, 이를 그대로 복제하는 문제
- Convolution representation으로 완벽히 수행할 수 있음(LTI property)
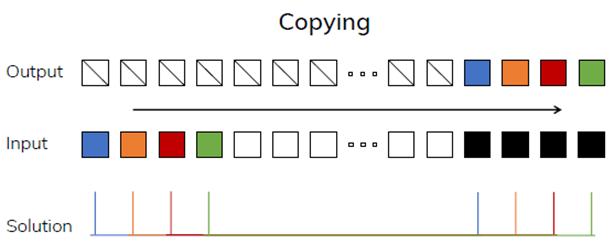
2. Selective Copying Task: Failure
- Copying task에서 기억해야 할 시쿼느의 순서를 무작위로 섞어놓고 복제하는 문제
- 관련 있는 토큰들(색칠된)을 기억하고 관련 없는 토큰들(흰색)을 걸러내기 위해서는 모델이 내용을 인식하는 추론 능력이 있어야 함
3. Induction heads: Failure
- 시퀀스 안에서 패턴을 인식하는 능력을 평가
- 첫 Layer에서 A1 -> B1라는 패턴을 발견했고, 다음 레이어에서 A2가 나타났을 때, 앞의 layer에서 induction으로 B2를 선택하는 경향이 있으면 Task에 성공하는것으로 간주
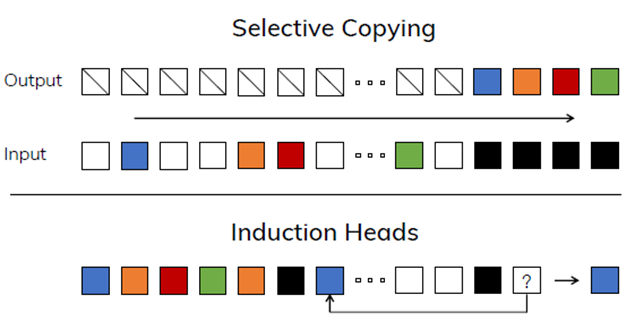
정리하자면 SSMs가 Representation learning 처럼 복잡한 패턴을 인식하지 못하고, Attention 처럼 시퀀스 내 Context를 이해할 수 있는 능력이 없다는 것이 밝혀졌습니다. 그 이유는 현재까지 봤던 SSMs이 LTI 즉, 시간에 따라 변하지 않는 동적 시스템을 가정했기 때문입니다. 즉, 시간이 지나도 그 시스템의 동장 방식이 변하지 않습니다.(A, B는 학습하는 파라미터가 아니었음)
이러한 특성 때문에 LTI 모델들은 주어진 맥락(Context)에서 올바른 정보를 선택하거나, hidden state에 시퀀스를 따라 전달되는 입력에 따른 변화를 주는 것이 어렵습니다.

그래서 저자는 SSM 구조를 발전 시켜서, 입력에 집중하거나 순차적 상태로 필터링 하는 Context aware한 능력을 갖는, 즉 선택성을 가질 수 있도록 제안하였습니다. 저자가 선택했던 방법은 기존에 고정시켜 놓았던 SSM의 파라미터인 B, C, Step size를 Linear projection해서 학습 가능한 파라미터로 만들어서, 시퀀스 사이의 관게에 영향을 주도록 하는 것입니다. 참고로, 여기서 학습 파라미터로 설정한 step size는 matrices를 discretize하는 과정에서 사용되는 step size입니다. 파라미터들이 학습 가능하기 때문에 시간에 다라 변하는 시변 SSM이 됩니다.(여전히 A는 고정 -> S4에서 사용한 matrix를 그대로 사용하는 것인가?)
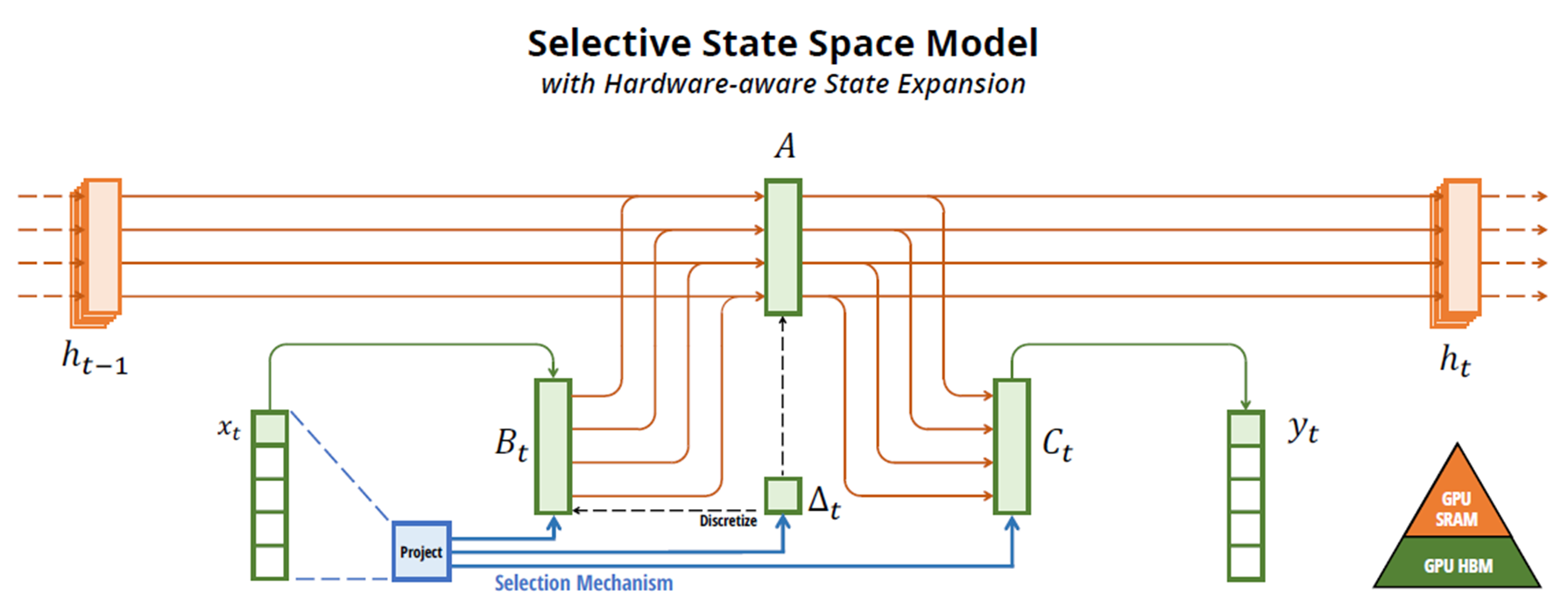
Selective state space model의 diagram 입니다. 전체 시퀀스를바탕으로 B, step size, C를 만들고, 이를 이용해 discretize한 후에, 원소를 하나씩 받아서 SSM 모델링을 진행하는 구조입니다. 이렇게 되면 원소가 순차적으로 입력이 될 때, 연산되는 B와 C는 전체 시퀀스가 반영된 matrix이기 때문에 모델이 Time invariant하지 않고, Time varying 합니다. 하지만, 원소를 순차적으로 하나씩 넣어주어야 하기 때문에, 기존에 SSM이 가지던 convolution mode는 기능을 상실하게 됩니다.Recurrent mode의 계산량은 O(BLDN)이고, Convolution mode의 계산량은 O(BLDlog(L))이라고 밝히고 있습니다. 표현을 효과적으로 하기 위해서 hidden state의 사이즈를 늘리면, convolution의 계산량이 더 적기 때문에 매우 효과적입니다. Selective state space model에서는 convolution을 사용하지 못하기 때문에, Recurrent mode만으로 representation을 효과적으로 할 수 있어야 합니다. hidden state의 사이즈를 무작정늘리고, 긴 시퀀스를 처리하려고 한다면 계산이 매우 힘들 것입니다. 따라서, 복잡한 패턴을처리하는 동시에 긴 시퀀스를 처맇기 위해서 3가지 techniques를 도입하였습니다.
- Kernel fusion
- Matrix multiplication을 제외한 모든 연산(Scan operation: 시퀀스를 하나씩 처리하는 과정)은 GPU HBM위에 올리고, GPU SRAM에 step size, A, B, C를 load 하고, 행렬 곱 연산 한후 output을 HBM에 기록합니다.
- Memory I/O를 크게 줄일 수 있다고 합니다.
- Parallel scan
- 이해를 못했어요ㅠ 도와주세요
- Recomputation
- Backpropagation을 위해 필요한 layer 별 hidden state의 정보를 저장하지 않고, backward pass 시 마다 재 계산하여 HBM으로부터 SRAM으로 load
- Memory 요구 사항을 줄일 수 있음
이 모든 과정은 위 Selective state space model 그림에 색을 달리하여 표현되어 있습니다.
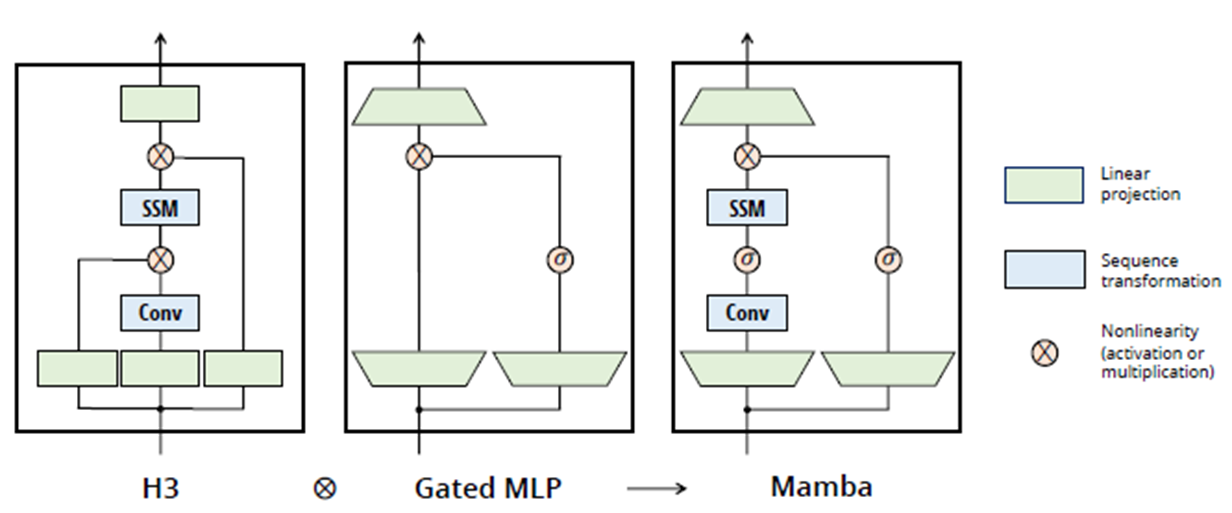
Mamba
Mamba는 기존에 우리가 코드로 봤던 Deep SSM의 구조를 경량화한 것을 의미합니다. 여기서 주의할 점은 만약 Mamba Architecture에 Selective method를 적용할 때에는 그림에 있는 Conv mode는 사용할 수 없습니다.
Experiement

왼쪽은 S4에서 실패했던 Task에 대한 성능입니다. S6은 selective method를 사용한 것입니다. 같은 Mamba 구조를 사용하더라도, S6을 쓴 것과 그렇지 않은 것 사이의 성능차이가 많이 보이는 대목입니다.
오른쪽은 시퀀스의 길이가 길어짐에 따라 Induction heads Task 성능이 어떻게 변하는지를 보여줍니다. 의심이 들 정도로 Mamba 성능이 압도적이네요..

시퀀스가 아주 길어지더라도 Mamba는 되게 강건하네요..
이상입니다. 긴 글 읽어주셔서 감사합니다.




