| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- irregularly sampled time series
- 패혈증 관련 급성 호흡곤란 증후군
- timellm
- pytorch
- nccl 업데이트
- moirai
- queueing theory
- 리뷰
- pre-trained llm
- 딥러닝
- multi gpu
- nccl 업그레이드
- GaN
- 분산 학습
- timesfm
- NTMs
- Time Series
- ed boarding
- 대기행렬
- gru-d
- ERD
- 의료정보
- first pg on this rank that detected no heartbeat of its watchdog.
- m/m/s
- nccl 설치
- 불규칙적 샘플링
- operation management
- 토픽모델링
- Transformer
- length of stay
- Today
- Total
데알못정을
[Review] The Impact of Delays on Service Times in the Intensive Care Unit 본문
[Review] The Impact of Delays on Service Times in the Intensive Care Unit
쩡을이 2024. 4. 24. 16:12Summary

이번 포스팅은 데이터 과학 분야가 아니라 매우 산업공학적인 내용을 다룹니다. 구체적으로, Operation Management 분야가 healthcare system에 어떻게 사용되는지 살펴볼건데, 바로 Queueing Theory를 이용한 분석입니다. 이번 포스팅에서 다룰 논문은 Queueing model을 사용하여 중환자실(ICU)입원을 위한 Waiting이 환자의 ICU length of stay에 미치는 영향을 분석하였습니다. 그 과정에서 delay의 효과를 체계적으로 구현하기 위해서, 기존 전통적 M/M/S queue 를 약간 변형한 M/M(f)/S를 제안하였습니다. 해당 논문은 INFORMS에 개제되어 있습니다.
Motivation

본 논문의 연구 동기에 대해 간단하게 말씀드리겠습니다. 우선 주요 queueing model은 다양한 health care setting에서 의료 서비스 제공을 모델링하는데 자주 사용되며, 더 나아가 운영적 결정을 내리는데 에도 사용이 됩니다. 이러한 queueing model의 대부분은 치료를 기다리는 환자가 경험하는 delay의 영향을 무시한다고 합니다. 하지만 delay를 오래 하면 할수록 환자에게는 부정적인 영향이 올 수 있고, 그에 따라 치료 받을 때 입원 기간(LOS)가 늘어날 수 있습니다. 따라서 본 논문에서는 ICU 입원을 위한 대기가 LOS에 미치는 영향을 분석하게 되었다 밝히고 있습니다.
- Study 1. Empirical Analysis - examining the impact of delays for patients being transferred from ED to the ICU
- Study 2. Modifying existing analysis and to present a theoretical analysis of them
이 연구에서는 크게 두 가지 실험 및 모델링을 통해서 분석적 인사이트를 도출하고자 하는데요, 먼저 첫 번째 Study에서 이미 수집되어 있는 데이터를 기반으로 ED boarding time이 ICU입원 후 LOS에 미치는 영향을 분석합니다. 이때 각 환자가 겪는 질병을 type별로 나누어서 분석을 하고, 이를 통해 질병 별 인사이트를 도출합니다. 예를 들어, 호흡기 질환을 가진 환자의 ED boarding time이 1시간 증가하면 LOS가 어떻게 되더라 ~ 식의 분석을 진행하는 것이지요. 두 번째 Study는 위 study 1인 경험적 분석에 나타난 현상이나 사실들을 설명하고, 이에 대한 이론적 분석을 제시하기 위해 이미 존재하는 queueing model을 발전시키는는 연구를 진행합니다. 이를 통해 delay가 LOS에 미치는 영향을 발굴하기에 아주 적합한 queueing model을 개발합니다. 앞으로 각 꼭지에 대해서 같이 살펴 볼텐데요, 이해를 돕기 위한 배경 지식은 중간 중간 같이 삽입하여 설명 드리겠습니다.
Study 1: Emprirical Analysis
첫 번째 Study에서는 이미 수집되어 있는 데이터를 기반으로 ED boarding time이 ICU입원 후 LOS에 미치는 영향을 분석합니다. 이러한 분석의 결과는 데이터를 기반으로 낸 통계적 결과이기 때문에, 향후 ICU에서 자원을 할당 및 계획에 응용될 수 있습니다. 특히 본 연구의 연구자들은 환자 ED에서 진단 받은 정보인 ICD9 code 10가지를 활용해서, ICU에서 치료되어 질 때 어떤 전문의에게 치료되는지도 반영을 했습니다. 이를 통해서, 특정 전문 영역에 대한 ED boarding이 LOS에 미치는 영향도 알 수 있도록 하였습니다.
사용한 데이터셋은 212,063명의 환자가 포함된 다 기관 데이터셋으로, 오픈 소스로 공개된 데이터는 아닌 것 같습니다. 각각의 waiting time을 고려하기 위해서 ED boarding time을 구하는 방법은 ED에서 측정된 마지막 관측치의 시점부터 ICU 입원 후 발견된 첫 관측치의 시점간의 차이를 이용했다고 밝히고 있으며, 이는 매우 합리적이라는 생각이 듭니다. 또한 특별하게 분석에 포함된 환자는 수술을 고려할 필요가 없는 환자들에 제한했습니다. 이는 waiting time이 미치는 영향만을 발굴하기 위해서 입니다. 이전에 언급한 환자의 10가지 질병은 암, 정신실환, 심장성 질환 등으로 이루어져 있습니다.

또한 환자의 LOS가 48시간 이상인 경우만을 포함 시켰는데요, 이는 48시간 이상 ED에 입원한 환자의 severity score 즉, 환자의 중증도를 평가하는 ESI 점수가 신뢰성이 있기 때문이라고 밝히고 있습니다. 더불어, 전체 LOS 의 분포의 식스시그마 범위 이상으로 넘어가는 LOS가 60일 이상이어서, 이를 이상치로 간주하고 제거하였다고 합니다. 그 결과 51,067 명의 ICU 비 입원 환자, 5,996 명의 ICU 입원 환자 기록을 보유할 수 있었습니다.

실질적으로 ED boarding 즉 waiting time이 LOS에 미치는 영향을 알아보기 위해 할 수 있는 가장 간단한 것은 선형 회귀식을 만드는 것입니다. 연구자들도 다음과 같은 식을 통해 선형 회귀식을 만들고자 하였는데요.
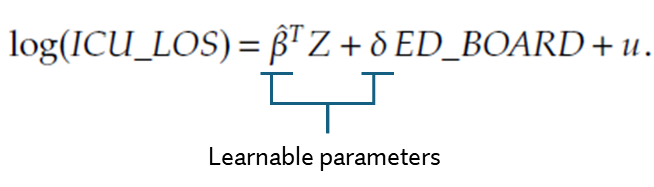
식에서 Z는 환자의 나이, 심각성, 입원 일 등이 될 수 있는 control variable이고, u는 가우시안 정규분포를 따르는 노이즈 항 입니다. 이러한 선형회귀식을 fitting하고 나면 회귀 계수 델타에 대한 해석을 통해 LOS에 미치는 영향을 알 수 있습니다. 만약 델타가 0보다 크다면 ED boarding이 일단 LOS에 영향을 미친다는 것을 의미하겠죠.
하지만, 해당 수식을 푸는 것에 대하여 몇 가지 통계적 이슈가 있습니다.
- 문제 1: Selection Bias
- ICU 입원 환자의 관측치 수가 ICU 비 입원환자 보다 매우 적음
- ICU에 입원을 해야만 ICU_LOS가 존재하기 때문에, 회귀 계수가 전체 모집단을 충분히 설명하지 못할 수 있음(잘못된 회귀식 도출)
- 이는 통계학에서 “선택 편향 문제”에 해당
- 문제 2: Endogenous Regressors
- ED_BOARD와 ICU LOS 모두에 미치는 관찰할 수 없는 요인이 있을 수 있음
- 예를 들어, 매우 심각한 환자에게는 우선 순위가 주어져 덜 심각한 다른 환자보다 먼저 ICU로 이송될 수 있으며, 그 환자는 결과적으로 LOS가 길어질 것임(ED_BOARD가 짧음에도)
- 이러한 심각도 요인을 관찰할 수 없는 경우 δ가 매우 편향될 수 있음
일반적으로 Endogenous regressors를 해결하기 위해 Instrumental variable을 도입합니다. 따라서 식을 아래처럼 수정할 수 있습니다.
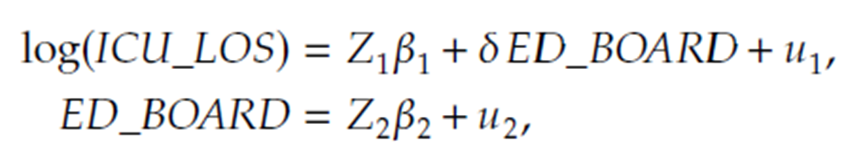
ED_BOARD 자체를 추정하고, 그 추정 값을 기반으로 LOS를 예측하는 구조입니다. 이때 Instrumental variable $Z_2$는 ED_BOARD 추정에 관련이 있으면서 동시에 LOS에는 영향을 주면 안되는 변수를 선정해야 합니다.
Selection bias 문제를 해결하기 위해서 Heckman 2 stage model이라는 통계 모델을 사용했습니다. 해당 모델은 1. Selection model, 2. Probit model로 전개될 수 있습니다.
- 1단계 Selection model
- 해당 선형 식의 값이 0보다 크면 ICU 입원을 의미하는 1, 아니면 0을 출력하게 하여 일단 모든 환자군을 고려하도록 함
- 이를 통해서 표본 선택 편의를 방지할 수 있음
- 이 모델은 현재 학습되고 있는 관측치가 어느 표본에서 나왔는지를 반영하는 장치(Inverse Mills Ratio)를 만들기 위한 선행 단계
-
주의*: 회귀식의 모든 오차항은 서로 독립이어야 함
-
그러나 ICU_ADM이 1이 되면 ρ≠0이 되며, ICU_LOS가 관측이 됨
-
즉, 오차 $u_1$과 $u_3$가 독립이라는 보장이 없음 → 선형 회귀 가정 중 일치성에 위배되며 회귀 계수 추정이 어려워 짐
-
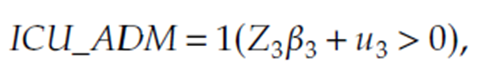
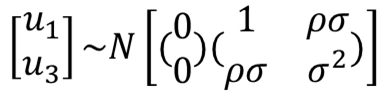
따라서 ICU ADM을 설명하는 $u_3$와 ICU LOS를 설명하는 $u_1$ 사이에는 다음과 같은 관계가 존재합니다.
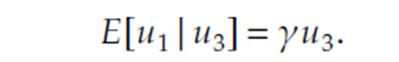
이전에 정의했던 회귀식을 다음과 같이 적절히 변형하고,

$E[u_1 |u_3] =γ u_3$, $E[u_1 |Z,ICU_ADM=1] =γ E[u_3 |Z, ICU_ADM = 1]$ 니까,
이때 $E[u_3 |Z, ICU_ADM = 1]$은 ICU ADM이 있었다는 것을 고려하여 다음과 같이 수정 가능합니다.
$$E[u_3│Z, ICU_ADM= 1]=E[u_3│u_3>-z_3 β_3 ]$$
2단계 probit model
$E[u_3│Z, ICU_ADM= 1]=E[u_3│u_3>-z_3 β_3 ]$에서 조건부 부분을 inverse mills ratio 형태로 나타낼 수 있다.
$=λ(z_3 β_3 )= φ(-Z_3 β_3 )/(1-Φ(-Z_3 β_3 ) )=φ(Z_3 β_3 )/Φ(Z_3 β_3 ) , where λ(⋅)=φ(⋅)/Φ(⋅)$
Inverse mills ratio가 현재 상황에서 의미하는 바는 해당 값이 클 수록 ICU에 입원하는 관측치가 드물다는 것을 의미합니다. 이를 통해, 회귀식 fitting에 사용된 된 샘플의 선택 편향을 샘플이 선택에서 배제되는 가능성을 고려하여 회귀식을 학습할 수 있습니다.
최종적으로 다음과 같은 회귀식이 도출될 수 있습니다.
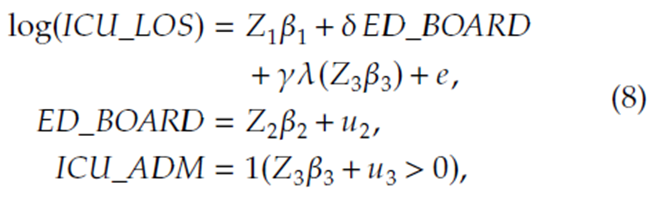
Control variable을 위해 사용된 변수는 논문에서 Table A.1에 제공하고 있습니다.
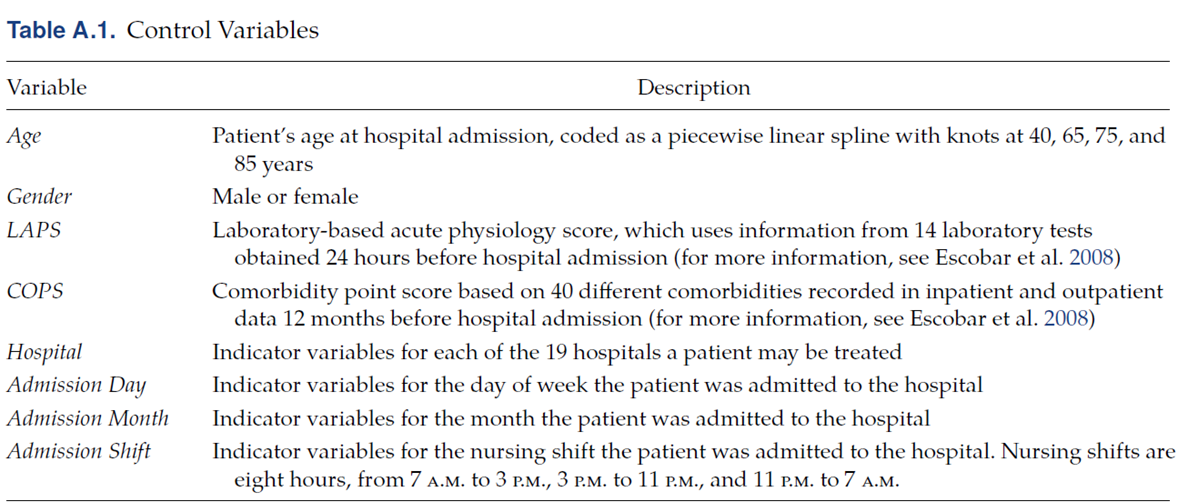
그 외에 $Z_2$의 경우에 ED_BOARD에 직접적인 관련이 있으면서 ED_BOARD를 통해 ICU_LOS에 영향을 줘야 하는 instrumental variable 이기 때문에 환자가 응급실에서 대기하는 동안의 평균 시간당 점유율(시간 별 응급실이 얼마나 많은 환자로 차 있었는지)을 congestion으로 정의하고, 이를 변수로 사용 했다고 추가적으로 밝히고 있었습니다. 또한 ICU 입원 여부를 결정하는 control variable로는 입원 병동 입원의 시간에서 ICU와 non_ICU의 congestion을 포함했다고 밝히고 있었습니다.
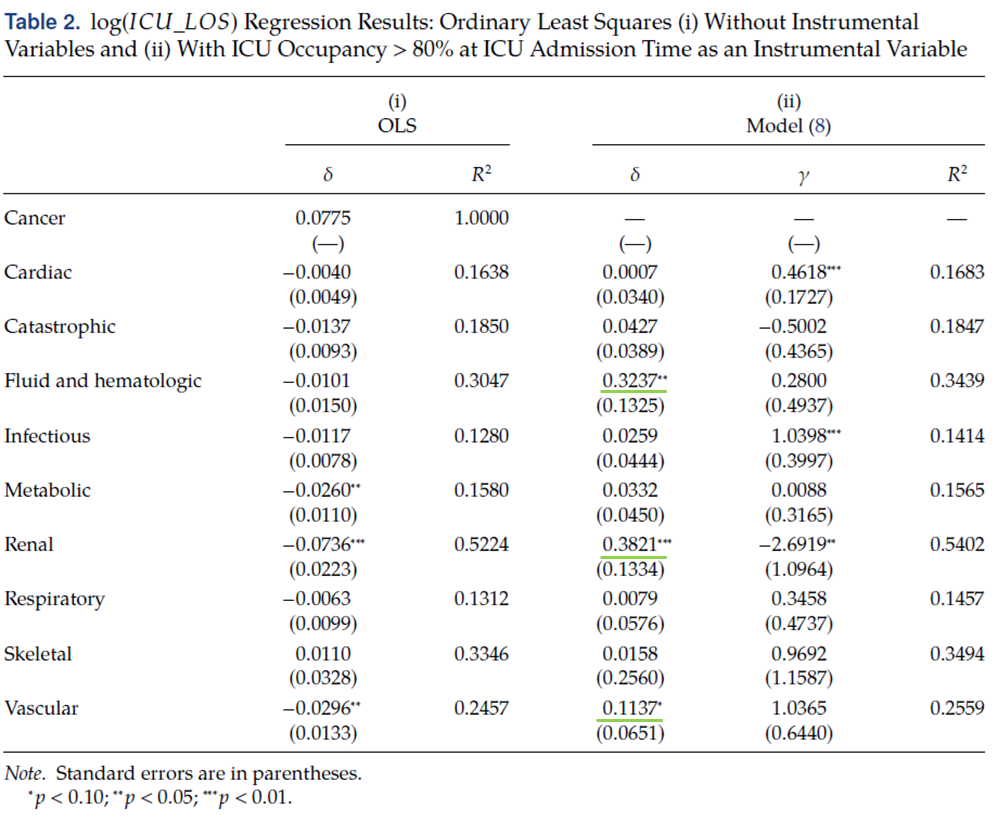
복잡한 과정을 거쳐서 얻은 회귀식의 적합 결과입니다. 일단, 일반적인 OLS로 한 것과, Heckman model을 이용했을 때 결과를 비교하고 있었습니다. Heckman model에서 선택 편향을 조정하는 파라미터인 $\gamma$가 유의미했던 patient caregory는 선택 편향의 증거를 나타냅니다. Renal의 경우, OLS를 사용했을 때, ED 대기 시간이 길 수록 LOS가 감소한다고 나타나는데, 이는 의학적 지식과 직관에 반하는 사실이었습니다. Model을 통해 통계적으로 유의미한 적합이 되었던 카테고리인 Fluid and hematologic, Renal, Respiratory의 경우 ED boarding이 1시간 증가할 때 ICU_LOS가 11 ~ 38 % 증가한다는 것이 나타났습니다. 그 나머지 type 들은 통계적으로 유의미하지 않았습니다.
1. Cancer, skeletal: ICU환자의 수가 매우 적었기 때문이라고 설명하고 있습니다.
2. metabolic: 650명의 환자가 있으나 delay가 아마도 ICU LOS 에 영향이 없을 것이라 분석했습니다. 그 이유는 대사는 당뇨, 면역장애, 신장 질병 말기 같은 만성 조건에 상응하며, 이러한 환자는 delay에 잘 견딜 수 있을 것이라 판단했다고 합니다.
3. Skeletal의 경우 치료되지 않고 남아 있는 경우 감영에 취약할 수 있으나, 그들의 긴급도가 다른 unit에 비해 낮은 경향이 있다고 설명하고 있었습니다.
Study 2: Queueing Model
현재까지, 본 논문에서 진행한 분석 2가지 중 1가지에 대해 설명을 드렸습니다. 방금 전까지의 분석을 통해 우리는 delay가 환자의 ICU LOS에 미치는 영향을 확인 했었는데요, 그렇다면 지금 부터는 구체적으로 delay가 잠재적으로 시스템에 어떤 영향을 주는지 밝힐 차례입니다. 본 논문에서는 M/M/S를 가정한 queueing system을 도입하였습니다. 논문에서 밝히지는 않았지만, 나름대로 저자들이 어떤 시스템을 모델링하고자 하는지 간단히 시각화 하면 아래 그림과 같습니다.

위 그림은 용량이 제한이 없는 queue 에서 환자들이 ED boarding을 하고 있는 상태입니다. 만약, ICU에 bed가 idle 하다면, 대기 하는 환자들이 대기한 순서대로 즉, FCFS 방식으로 bed에 들어 갑니다. 여기서 서버 즉, bed의 service time은 각 환자의 LOS가 되는 것이지요. 우리는 해당 논문에서 새롭게 개발한 M/M/S 시스템에 대해 이해를 하기 앞서, 간단히 Queueing에 대해 알아보겠습니다.
- Queueing Theory
- 서비스를 제공받기 위해 기다리는 것은 피할 수 없음
- 부품은 다음 공정으로 넘어가기 전에 대기를 함
- 항공기들은 착륙 허가를 받기 위해 공중에서 선회 함
- 서비스 시설을 추가로 설치하고 운영하는 것은 비용을 유발하고, 고객이 경험하는 대기 비용으로 만족도가 결정되기 때문에 위 두 비용 간의 균형을 취하는 것이 유일한 방법임
- Queueing model의 구성요소
- Customer: 서비스를 받고자 하는 주체(patient, car, parts)
- Server: 서비스를 제공하는 주체 (ICU Bed, Parking lot, Semi conductor Process)
- Customer는 바로 Service를 받기 시작하거나, 시설이 서비스 중이면 Queue에서 대기
- Customer는 도착 시간 간격(Interarrival time)을 갖고 시스템에 도착
- Server는 고객 당 서비스 시간(Service time)을 갖고 작업을 처리
- Interarrival time과 Service time은 확률적(e.g. 우체국 운영)이거나 확정적(e.g. 의사와 예약)
- Queueing Discipline: FCFS(선입선출), LCFS(후입선출), SIRO(무작위 순서)
M/M/S queue란, queueing model이 M/M/S로 라벨링 된 것인데요. 라벨링 규칙은 아래와 같습니다.
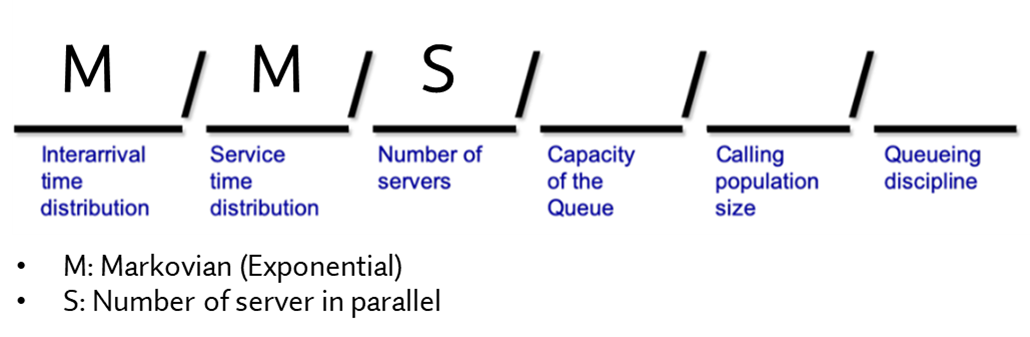
제일 왼쪽 칸에 고객 도착 률 $\lambda$이 어떤 분포를 따르는지 써주고, 그 다음 칸에는 service time $\mu$이 어떤 분포를 따르는지 써줍니다. 그리고 그 다음 칸에는 총 서버의 수를 적어주는 것이죠. 이러한 배경지식 하에, M/M/S를 이해해보면 다음과 같이 요약할 수 있겠습니다.
"고객의 도착 간격이 Exponential distribution을 따른다. 고객 당 서비스 시간은 Exponential distribution을 따른다. 서버의 수는 S개 이다."
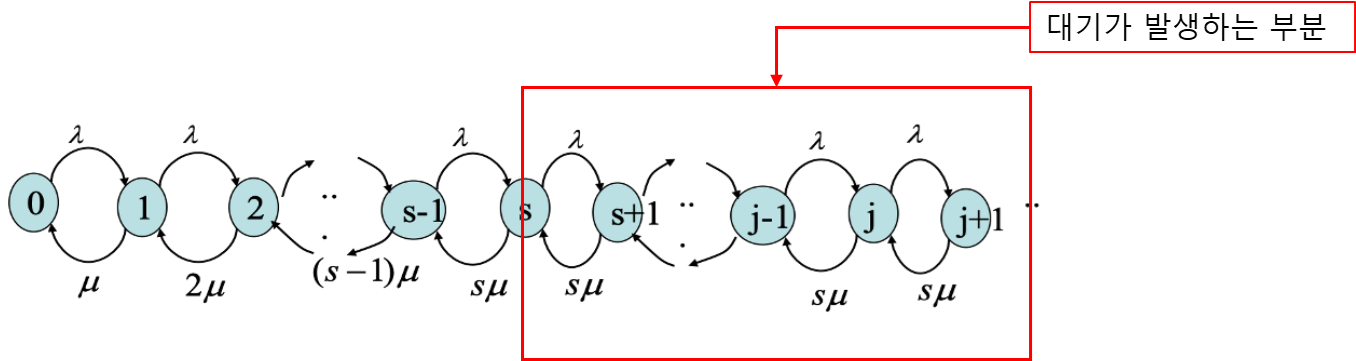
이렇게 만들어 놓은 모델을 가지고 할 수 있는 분석에 대해 설명 드리겠습니다. 사실 이런 diagram 안에는 많은 정보가 포함되어 있는데요, state 0에서 1로 이동하려면 사실 state 0에서 1로 전이할 확률을 곱해주어야 합니다. 이때 중요한 것은 자기 자신으로 이동하는 확률은 0입니다. 그러고 들어오는 양은 나가는 양이다 즉, balance equation을 통해 식을 전개하다 보면, steady state를 보일 수 있습니다. 즉, 시스템의 steady state는 모든 전이 확률이 수렴하는 순간입니다.
이 상태를 만들어 놓으면, 해당 시스템의 performance를 측정할 수 있습니다. 기본적인 performance measure는 아래와 같습니다.

L, W 들은 Little's law에 의해 서로 변환 가능합니다.
이제 우리는 MMS에 대해 간단한 이해를 하고 있으니, 본 논문에서 M/M/S를 문제 상황에 맞게 수정한 MM(f)S가 어떻게 동작하는지 알아보겠습니다. 먼저, 본 연구에서는 고객의 도착률과 서비스율이 모두 지수분포를 따른다고 가정하고 있습니다. 또한 저자는 경험적 study를 통해 Delay, 즉 waiting이 시작됨에 따라 서비스 시간인 LOS가 달라진다는 것을 발견했고, 이것의 작동 과정을 살펴볼 것이기 때문에, 대기행렬모형에서도 서비스 율을 delay에 종속적인 관계를 갖게 하도록 inflation function으로 수정하여 M(f)로 표기했습니다.
따라서 service time 은 평균이 $1+ f(N_t)$인 지수분포를 따른다고 가정했습니다. 참고로 $N_t$는 t 시점의 서비스 안에 있는 job 즉, 환자의 수 입니다 즉, state를 나타냅니다. 만약, 시스템 내 환자가 없다면, inflation 함수는 0의 값을 갖고, 서비스 율 $\mu$는 1이 됩니다. 그렇지 않다면, service time은 $f$가 증가함에 따라 증가할 것이고, 결국 delay가 길어질 수록 더 낮은 service rate을 갖게 되어 단위 시간당 처리하는 service time이 길어져 시스템이 과부하가 되는 것입니다. 따라서 저자가 의도한 대로 delay의 수준에 따라 service rate이 변화하게 됩니다. 저는 이를 diagram으로 나타내면 대충 아래 그림과 같을 것이라고 생각했습니다.
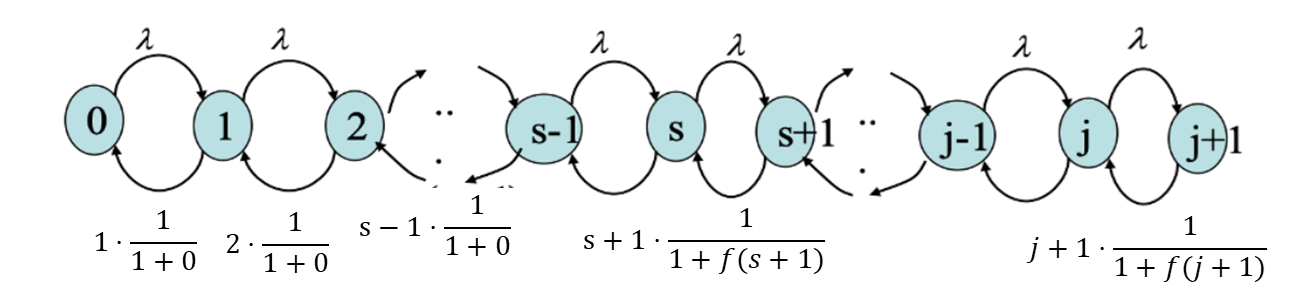
안정 상태를 가지는 queueing 을 가지고 성과 측정을 하기 때문에 이렇게 만든 queueing model 이 안정상태를 가질 수 있는지 확인해야 합니다. 저자는 우선 inflation 함수인 f가 가질 수 있는 가장 큰 값에서 unstable한지 먼저 확인했습니다. 크게 두 가지를 검증했는데, 이 두가지는 시스템이 불안정해질 수 있다는 근거가 되었습니다.

결론적으로, 시스템이 불안정해지는 순간이 있으므로 해당 모델은 week stability를 갖는다 하는데, 이럴 수 있는지는 잘 모르겠으며, 수식을 이해하지 못했습니다. (ㅠㅠ)
M/M(f)/S의 불안정 상태 가능성을 확인하고서 생각할 수 있는 것은 만약 환자가 몰려서 도착을 하게 될 경우 환자들은 최악의 수준의 delay와 ICU LOS를 겪을 것이며 이런 경우 시스템은 최대의 서비스 시간을 요구 받고, 모든 환자는 delay되는 지점까지 매우 빠른 속도로 악화될 것입니다. 그러므로 stability는 환자의 수를 제한하는 것에서 이룰 수 있습니다. 그래서 저자는 이러한 한계 때문에, short term 동안 시스템을 분석해야 한다면서 이 점을 한계점으로 남겨두었습니다. 따라서 앞으로 나오는 분석 내용 시스템이 최대로 부하되었을 때(f가 supremum 일때)를 최대한 근사하는 식으로 model을 구현하는 것입니다.
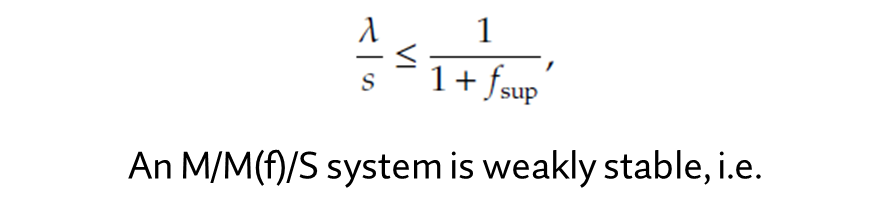
이번 장표는 M/M(f)/s system이 안정상태일 때 성과 측정을 다룹니다. 본 논문에서는 workload라 하는 것을 지표로 하였는데, 이는 작업량으로, 정확하진 않지만, 그 의미 상 시스템 내 임상의, 의료진들이 겪는 작업의 양으로 유추할 수 있으며, 이는 곧 Queueing 이론에서 다루는 안정상태 성과 측정 지표 중 시스템 내 고객의 수로 근사할 수 있다고 생각했습니다. 논문에서 구체적인 의미를 밝히지 않고 있어서 이렇게 이해를 하게되었는데, 그 이유를 나중에 알려드리겠습니다. 시스템이 안정 상태 일 때 성과 측정을 근사하는 과정에서 총 세가지 모델이 사용됩니다. 각각의 Notation은 아래와 같습니다.

성과 측정 근사 과정 중에, 논문에선 우선 이전에 언급한 infliation function을 간단하게 $k$로 둔 특별한 케이스에 대해 살펴보고, 이를 일반화 하는 흐름을 갖습니다. 해당 과정의 증명 과정을 생략하겠습니다. 해당하는 아래 식을 이해해보면, 환자가 ICU 입원을 위해 기다릴 때, ICU bed가 Inflation 된 상황에서는 caregiver가 겪는 작업의 양이 매우 클 것으로 예상할 수 있는데, 만약 어떤 환자가 도착했는데 운이 좋게도 기다릴 필요 없이 ICU에 입원할 수 있다고 했을 때는 Caregiver가 실제로 겪는 작업의 양이 줄어들 수 있습니다.
이 경우를 고려하여 논문에서는 미리 예상한 작업량보다 실제 환자가 caregiver에게 준 작업량이 더 적을 수 있다는 것을 반영하겠다고 하고 있습니다. 즉, 전체적으로 정리하자면, 결론적으로 $E[W]$를 찾겠다는 것은 시스템이 과부하 되지 않는 선에서 시스템의 안정 상태를 찾겠다는 것과 동치가 됩니다.

따라서 이 Upper bound를 일반화 하기 위해서, 새로운 고객의 도착 m을 제한함으로써 M/M(f)/S system을 근사할 수 있는 것입니다.

현재 Bound의 Term 들이 파라미터 $k$와 $\lambda$에 의해 좌우되고 있기 때문에 민감도 분석을 진행했습니다.
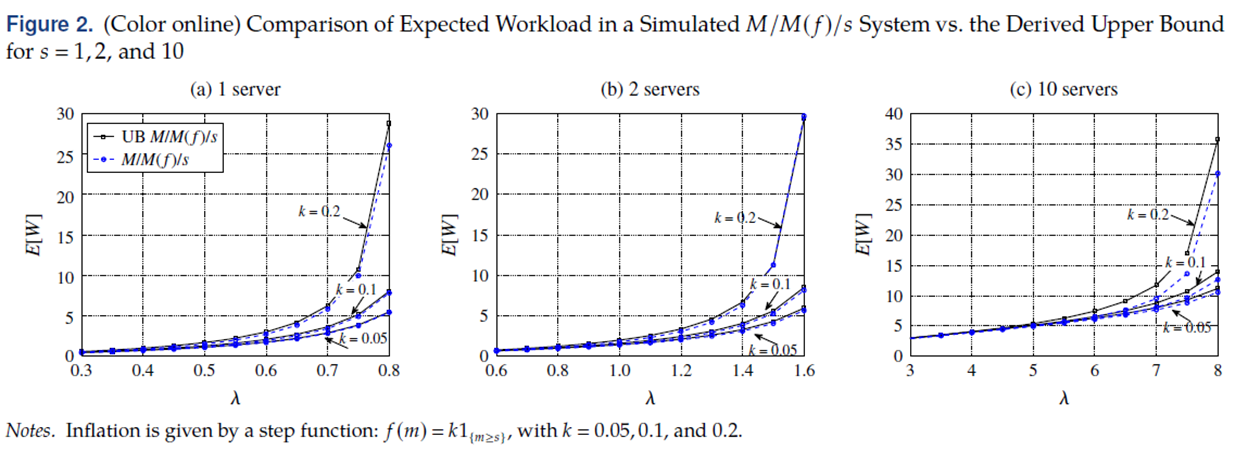
일단, 그림에서 파란색은 시뮬레이션을 통해 얻은 모델로, 논문에서는 비교할 대상으로 보고있습니다. 그렇다면 이 figure 를 통해 알 수 있는 사실은 전체 figure에서 대부분 시뮬레이션 한 M/M/(f)s와 upper boud를 통해 모델링한 저자의 모델이 거의 비슷하다는 것인데, 이는 upper bound 방식으로 M/M(f)/S 시스템을 근사한 것이 delay dependent sytem을 잘 모델링 함을 알 수 있습니다.
그림에서 고객 도착률이 변함에 따라 workload가 어떻게 변하는지 살펴보면, 고객의 도착률이 높아질 수록 workload가 기하 급수적인 상승을 나타내며 변화하고 있습니다. 이는 delay effect를 고려할 경우 workload가 빠르게 증가하는 것을 의미합니다.
일반적으로, M/M/S에서 server의 수 s와 고객 도착률 $\lambda$가 변함에 따라 workload의 민감도는 $1/(1-\rho)$ 곡선을 그리며 변화한다 알려져 있습니다. 그러나, Delay effect를 고려한 M/M(F)/S의 경우 M/M/S보다 더 빠르게 변화하고 있습니다. 이를 2가지 Case에 대해 살펴보고, 수식적으로 증명하면 아래와 같은 결과를 얻을 수 있습니다.
Case 1. The single server M/M/1 vs M/M(f)/1
Delay를 고려했을 때, 그렇지 않았을 때 정확히 어느 수준으로 workload가 증가할 수 있는 지 알기 위해 첫 번째로 저자는 delay를 고려하지 않은 single server M/M/1 과 delay를 고려한 M/M(F)/1간의 workload의 비율을 조사했습니다. 그리고 논문에서 일반 M/M/1 시스템의 workload의 기댓 값을 다음과 같이 나타냈는데요, 저는 여기서 workload가 결국에 long range average number of custormer in system과 같다는 것을 알게 되었습니다. 왜냐하면 arrival rate $\lambda$ 가 1이고, $\mu$가 1인 M/M/1 의 $L$을 계산하면 똑같이 나오거든요.
$$E[▁W] =ρ/((1-ρ) $$
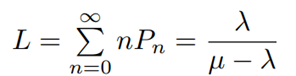
아무튼 upper bound 를 사용하여 근사한 M/M(f)/1로 도출한 workload를 $W^UP$라 했을 때, 두 모델의 workload 관계는 다음과 같이 증명됩니다.
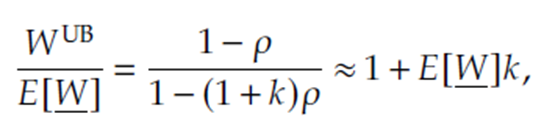
즉, 지연 효과를 고려할 때 일반 M/M/1 system의 기대 workload 보다 더 M/M(f)/1이 더 상승하며, $E[ \underline{W}]$가 $1/(1-\rho)$에 따라 상승하는 점을 감안했을 때, 지연 효과를 고려하면 $1/(1-\rho)^2$에 따라 증가할 것이라는 걸 알 수 있습니다.
Case 2. The Two-Server Case M/M/2 vs M/M(f)/2
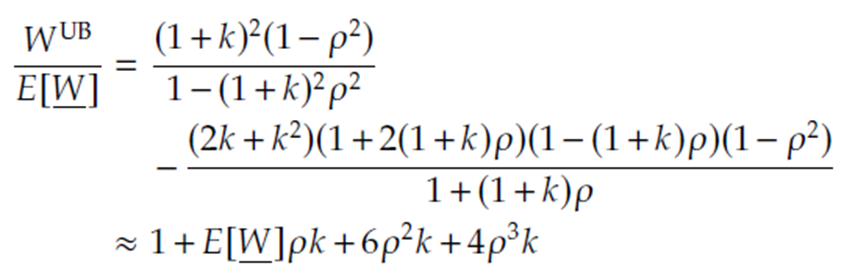
서버의 갯수를 2개로 늘려서 평가해 보았을 때도, 서버가 1개일 때와 같은 결과가 나왔습니다.( 지연 효과를 고려하면 $1/(1-\rho)^2$에 따라 증가)
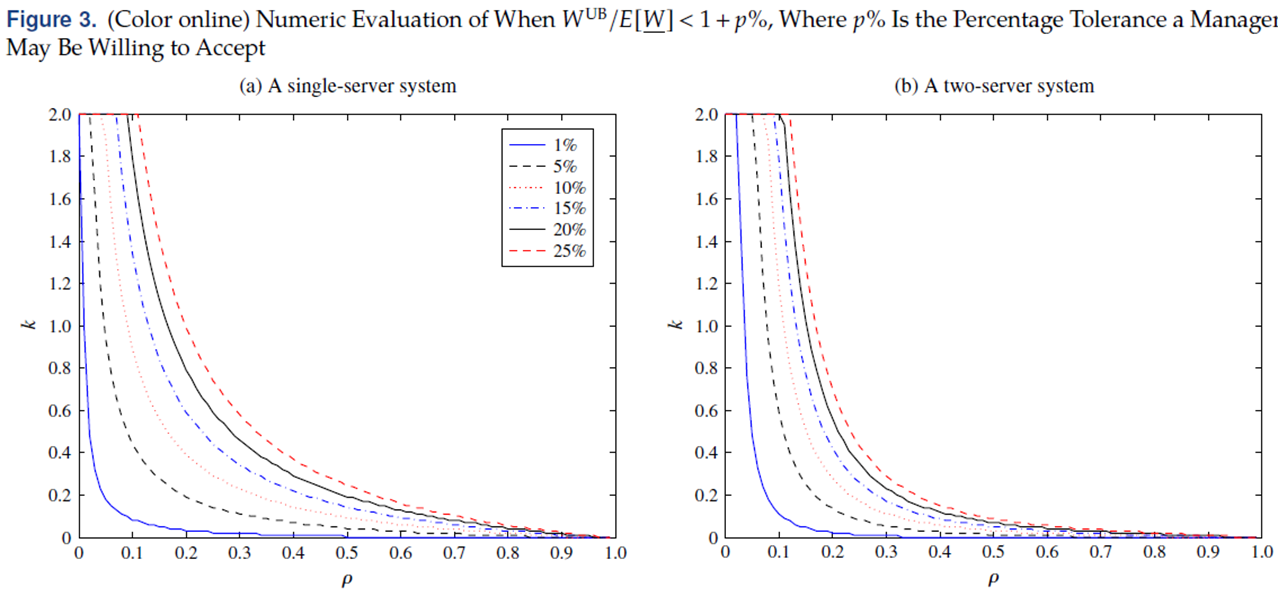
즉 기존의 전통적 큐잉 모델이 헬스케어 세팅에서 용량 관리와 성능 평가에 사용된 것은 맞지만, 에서 delay를 고려한 결과를 보았을 때, 기존 큐잉 모델들은 실제 임상에서 겪을 수 있는 delay를 상당부분 과소평가할 수 있다는 것입니다.
이러한 효과는 utility를 의미하는 $\rho$와 inflation 인자 $k$를 크게 키울 때 더 극명하게 나타납니다. 먼저 싱글 서버의 경우 지연 효과를 고려하지 않을 때와 고려할 때의 차이를 10% 정도를 작게 유지하려면 실제 임상에서 $\rho$가 0.3 보다 작고, $k$가 0.2보다 작아야합니다.
서버가 2개일 경우 지연 효과를 고려하지 않을 때와 고려할 때의 차이를 10% 정도를 작게 유지하려면 실제 임상에서 $\rho$가 0.15보다 작고, $k$가 0.4보다 작아야합니다. 하지만, 대부분의 임상에서는 $\rho$가 65%에서 90%사이에 있는 경향이 있으므로 Delay를 고려하지 않고, 시스템 결정에 사용하기는 매우 비현실적이라는 것 을 시사합니다.
여기에 더불어, 우리가 위에서 했었던 empirical analysis에 기반하여 patient category중 skeletal의 경우 ED boardinG이 LOS에 미치는 영향이 없을 뿐 아니라, 환자의 수가 매우 적기 때문에, delay를 고려하지 않은 MMS를 사용해도 되는 조건이라고 밝히고 있었습니다. 그에 반해, Fluid and hematologic 같은 type의 경우에는 ED boarding이 ICU LOS에 강한 인과관계가 있었으므로, 이 경우에는 전통적 M/M/S를 사용할 경우 부정확한 예측이 될 것이라는 것이라 분석했습니다.
M/M(f)/S in real system
이후 성과 측정을 및 비교를 위해 3가지 버전의 모델을 사용했습다.
- 1. M/M/S with $ρ =λ$(즉., $ρ=λ/(μ=1)$)
- This represent a traditional queueing system without delay effect
- 2. M/M(f)/S with $ρ =(1+k)λ$(즉., $ρ=λ/(μ=1/(1+k))$)
- This represent a queueing system where the amount of work each job brings is artificially inflated as if all jobs experienced delays.
- 이 경우 $f(⋅)$이 supremum(sup)인 상황(시스템 과부하)
- 3. Upper bound derived M/M(f)/S
- 본 논문에서 추정한 M/M(f)/S
- Theorem 2.
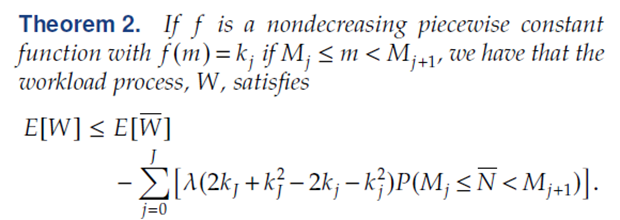
여기서는 이제 inflation function에 넣은 인자 $k$를 결정해야한다. 이를 위해 위에서 진행했던 empirical study의 결과를 기반으로 선정했습니다.
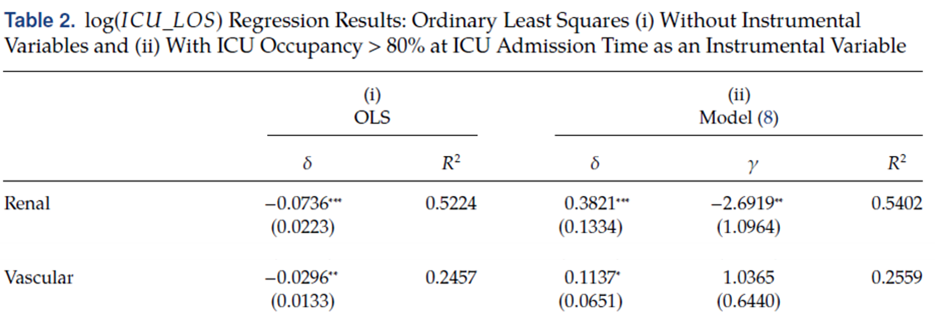
현실 시스템에 모델을 반영하는데 앞서, 저자는 혈관 및 신장 환자에 중점을 두었습니다. 그 이유는 delay 시 ICU LOS의 통계적으로 유의미한 증거가 있었던 집단이며, 가장 그 수준이 가장 낮고, 높은 집단이기 때문입니다. 저자는 앞으로 실험에서, ED_BOARD가 ICU_LOS에 기여하는 수준이 낮더라도 delay를 고려했을 때 어떻게 될지 보고 싶었던 것 같습니다. 위 정보 요약을 하자면, 신장의 경우 ED 대기 1시간 당 ICU LOS 38%가 증가하는 것으로 나타났고, 혈관의 경우 11.37%가 증가하는 것으로 나타 났엇습니다.
1. Vascular patients
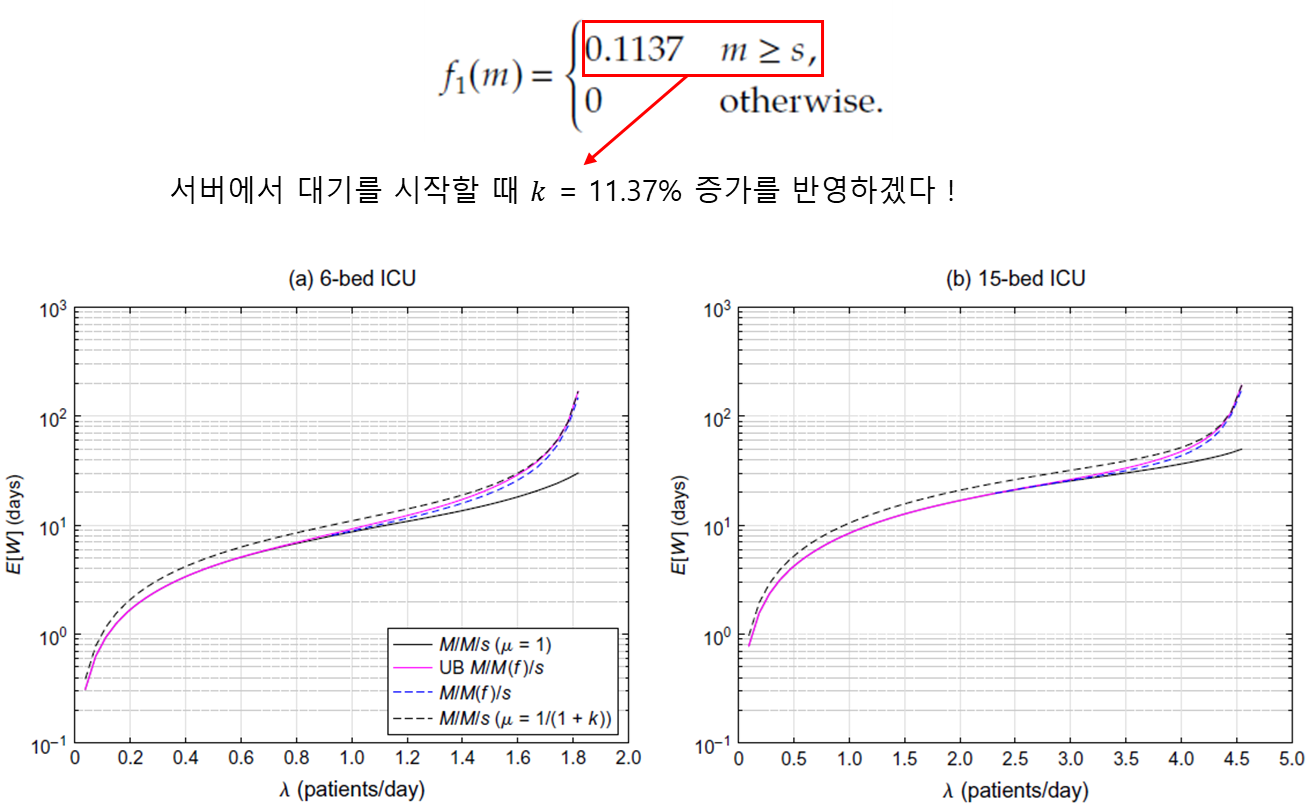
여기서 발견할 수 있는 사실은 먼저 우리가 M/M(f)/S의 upper bound를 추정하여 모델링한 분홍색 선이 실제 M/M(f)/S와 크게 다르지 않았다는 것을 통해 우리의 시스템이 불안정한 M/M(f)/s를 그래도 잘 추정했다는 것을 의미합니다. 또한, Vascular type은 매우 작은 delay를 갖는 category임에도 불구하고, 고객의 도착률이 증가할 수록, 어느 순간부터 delay를 고려하지 않은 M/M/S 와 꽤 차이가 나는 경향이 있다는 것입니다. 이는 delay를 고려하지 않으면 실제 작업업량을 misleading할 수 있음을 의미합니다. 이는 향후 의사결정에 큰 영향을 줄 수 있습니다.
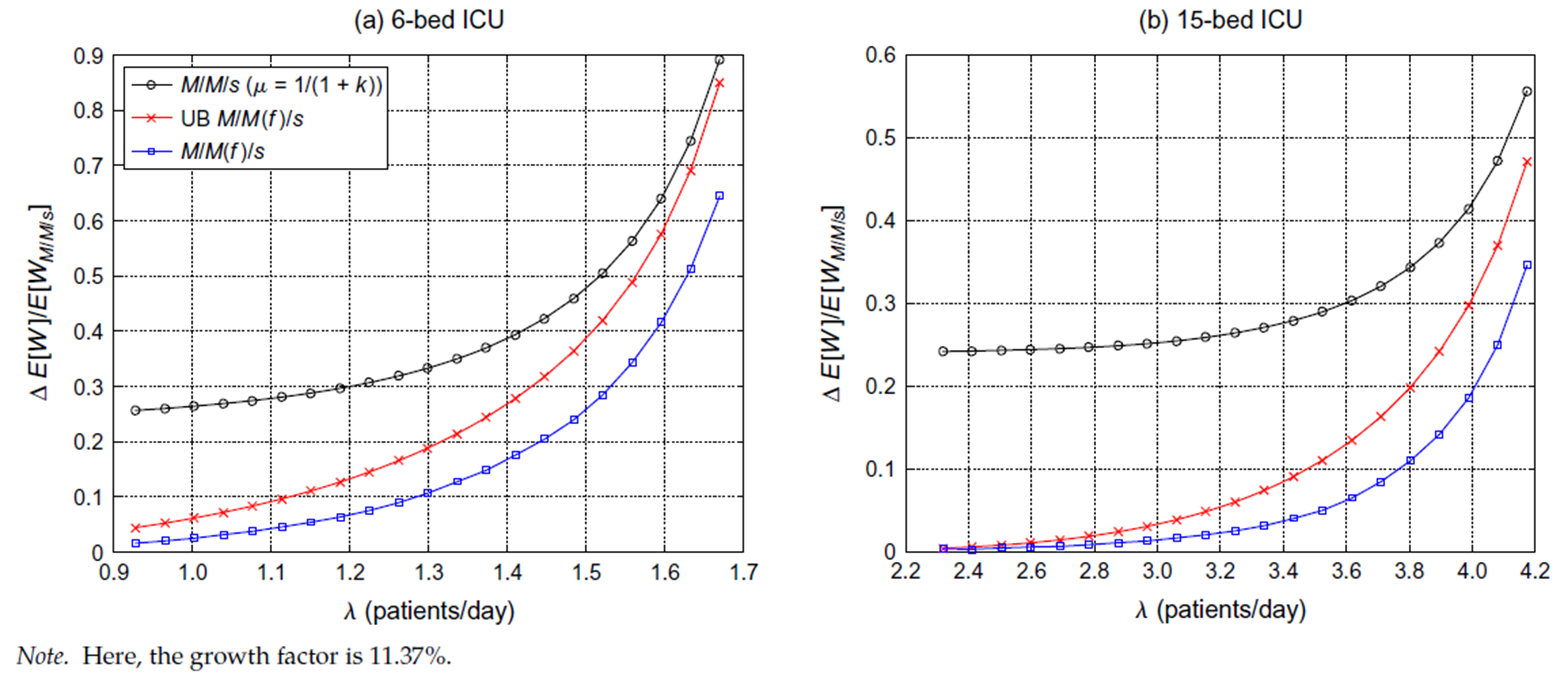
이 그림은 Y 축을 조금 수정한 것입니다. 그러니까 전통적 MMS 모델에 비해 작업량이 얼마나 증가했는지를 고객의 도착률 변화에 따라 시각화 한 모습입니다.이전 그림 보다 극명한 차이를 보이게 하나, 기본적으로 비슷한 해석을 할 수 있습니다.
2. Renal patients($f_2 (m)=0.3821$)
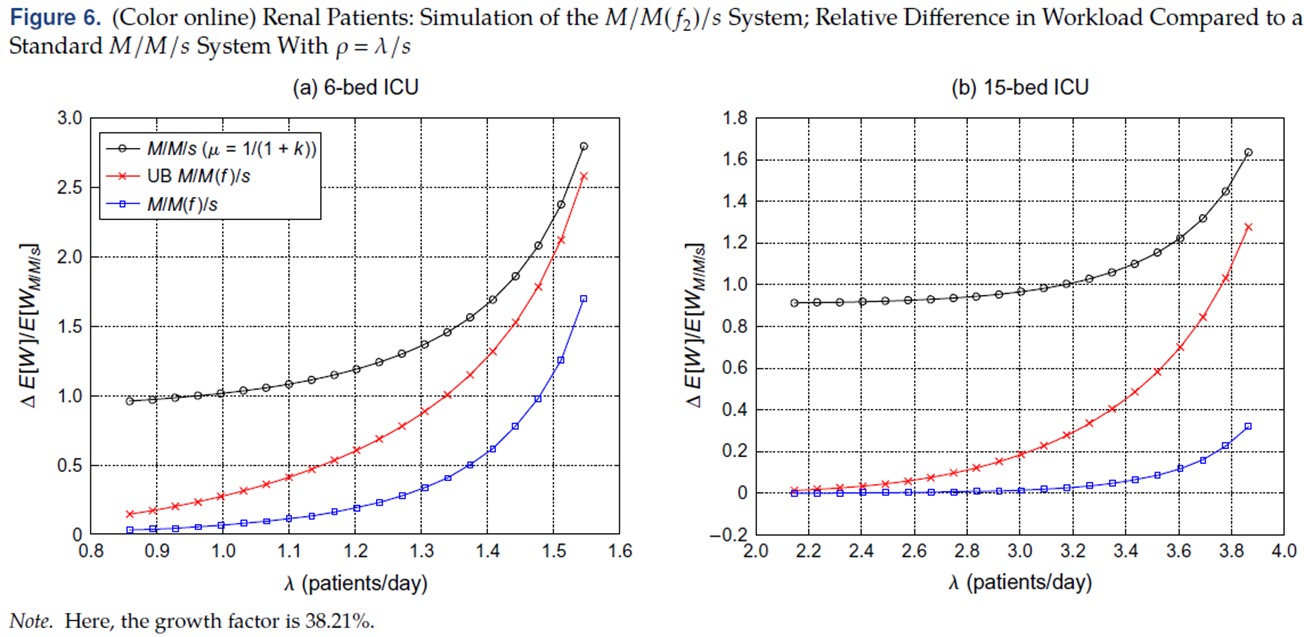
그림에서와 같이, 빨간색 선(우리의 모델)이 살짝 느슨하다는 것을 알 수 있습니다. 논문에서는 이를 upper bound가 단일 작업이 가져오는 작업만 고려하고, 향후 작업이 max만큼 지연할지, 아닐지에 대한 전파 효과를 고려하지 않았기 때문이라고 설명하고 있습니다. 그래서 이를 해결하기 위해 $f$를 더 복잡하게 가져가는 시도를 합니다. 이 부분부터는 이해가 도저히 가지 않았습니다 (ㅠ)
마무리
본 논문을 한마디로 정리하자면 "ICU 입원을 앞둔 환자의 대기 시간이 ICU LOS에 미치는 영향을 분석하기 위해 Delay를 고려할 수 있는 M/M(f)/S queueing model을 제안" 했다.
Delay를 고려한 모델이 그렇지 않을 때 보다, workload 에서 큰 차이를 보였다. 이 모델은 delay를 반영함으로써 현실 세계를 최대한 묘사했는데 이를 통해 올바른 정보를 caregiver에게 전달하고, 올바른 계획을 세울 수 있게 할 수 있다.(Insight)
-끝-




